Home » date » 2009 » Dec » 20 »

Model 4

*The author of this computation has been verified*

R Software Module: /rwasp_multipleregression.wasp (opens new window with default values)

Title produced by software: Multiple Regression

Date of computation: Sun, 20 Dec 2009 04:10:48 -0700

Cite this page as follows:

Statistical Computations at FreeStatistics.org, Office for Research Development and Education, URL http://www.freestatistics.org/blog/date/2009/Dec/20/t12613076061whrt61i4saljbh.htm/, Retrieved Wed, 22 May 2013 11:11:48 +0000

Original text written by user:

IsPrivate?

No (this computation is public)

User-defined keywords:

System-generated keywords (parent):

(pk = 0)

Estimated Impact

Dataseries X:

» Textfile « » CSV « » Correlation Matrix « » Notched Boxplots «

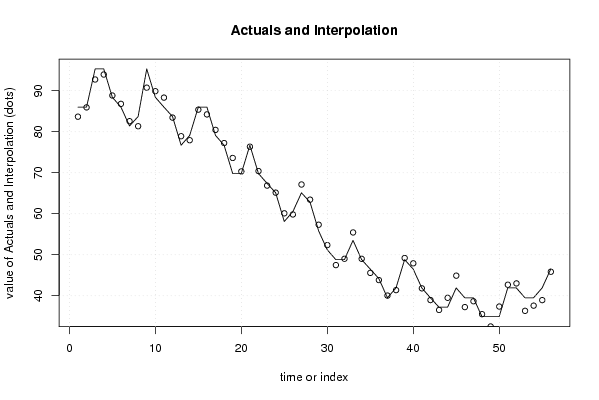
86,0	88,4	90,7	95,3	100,0	94,7
86,0	86,0	88,4	90,7	95,3	110,6
95,3	86,0	86,0	88,4	90,7	71,3
95,3	95,3	86,0	86,0	88,4	104,1
88,4	95,3	95,3	86,0	86,0	112,3
86,0	88,4	95,3	95,3	86,0	110,2
81,4	86,0	88,4	95,3	95,3	112,9
83,7	81,4	86,0	88,4	95,3	95,1
95,3	83,7	81,4	86,0	88,4	103,1
88,4	95,3	83,7	81,4	86,0	101,9
86,0	88,4	95,3	83,7	81,4	100,4
83,7	86,0	88,4	95,3	83,7	106,9
76,7	83,7	86,0	88,4	95,3	100,7
79,1	76,7	83,7	86,0	88,4	114,3
86,0	79,1	76,7	83,7	86,0	73,3
86,0	86,0	79,1	76,7	83,7	105,9
79,1	86,0	86,0	79,1	76,7	113,9
76,7	79,1	86,0	86,0	79,1	112,1
69,8	76,7	79,1	86,0	86,0	117,5
69,8	69,8	76,7	79,1	86,0	97,5
76,7	69,8	69,8	76,7	79,1	112,3
69,8	76,7	69,8	69,8	76,7	106,9
67,4	69,8	76,7	69,8	69,8	120,9
65,1	67,4	69,8	76,7	69,8	92,7
58,1	65,1	67,4	69,8	76,7	110,9
60,5	58,1	65,1	67,4	69,8	116,5
65,1	60,5	58,1	65,1	67,4	77,1
62,8	65,1	60,5	58,1	65,1	113,1
55,8	62,8	65,1	60,5	58,1	115,9
51,2	55,8	62,8	65,1	60,5	123,5
48,8	51,2	55,8	62,8	65,1	123,6
48,8	48,8	51,2	55,8	62,8	101,5
53,5	48,8	48,8	51,2	55,8	121,0
48,8	53,5	48,8	48,8	51,2	112,2
46,5	48,8	53,5	48,8	48,8	126,0
44,2	46,5	48,8	53,5	48,8	101,8
39,5	44,2	46,5	48,8	53,5	117,9
41,9	39,5	44,2	46,5	48,8	122,2
48,8	41,9	39,5	44,2	46,5	82,7
46,5	48,8	41,9	39,5	44,2	120,5
41,9	46,5	48,8	41,9	39,5	120,3
39,5	41,9	46,5	48,8	41,9	134,2
37,2	39,5	41,9	46,5	48,8	128,2
37,2	37,2	39,5	41,9	46,5	100,5
41,9	37,2	37,2	39,5	41,9	126,0
39,5	41,9	37,2	37,2	39,5	122,9
39,5	39,5	41,9	37,2	37,2	106,1
34,9	39,5	39,5	41,9	37,2	130,4
34,9	34,9	39,5	39,5	41,9	121,3
34,9	34,9	34,9	39,5	39,5	126,1
41,9	34,9	34,9	34,9	39,5	88,7
41,9	41,9	34,9	34,9	34,9	118,7
39,5	41,9	41,9	34,9	34,9	129,3
39,5	39,5	41,9	41,9	34,9	136,2
41,9	39,5	39,5	41,9	41,9	123,0
46,5	41,9	39,5	39,5	41,9	103,5

Output produced by software:

Enter (or paste) a matrix (table) containing all data (time) series. Every column represents a different variable and must be delimited by a space or Tab. Every row represents a period in time (or category) and must be delimited by hard returns. The easiest way to enter data is to copy and paste a block of spreadsheet cells. Please, do not use commas or spaces to seperate groups of digits!

Summary of computational transaction
Raw Input	view raw input (R code)
Raw Output	view raw output of R engine
Computing time	5 seconds
R Server	'Gwilym Jenkins' @ 72.249.127.135

Multiple Linear Regression - Estimated Regression Equation

Werkloosheid(Y(t))[t] = + 2.85103732321234 + 0.976127794666543`Y(t-1)`[t] + 0.236365899150279`Y(t-2)`[t] + 0.134593358559729`Y(t-3)`[t] -0.341976205796012`Y(t-4)`[t] -0.0864265177172897Productie[t] + 2.5704281506859M1[t] + 8.0452757771165M2[t] + 10.6852562679373M3[t] + 5.13454323216124M4[t] -2.36138688814796M5[t] + 0.840375791480767M6[t] + 3.94041195459863M7[t] + 7.0899908939364M8[t] + 13.9240510104693M9[t] + 0.826377650593013M10[t] + 1.18103914539342M11[t] + 0.0648222506919648t + e[t]

Multiple Linear Regression - Ordinary Least Squares
Variable	Parameter	S.D.	T-STAT H0: parameter = 0	2-tail p-value	1-tail p-value
(Intercept)	2.85103732321234	10.306593	0.2766	0.783569	0.391784
`Y(t-1)`	0.976127794666543	0.151884	6.4268	0	0
`Y(t-2)`	0.236365899150279	0.217164	1.0884	0.283264	0.141632
`Y(t-3)`	0.134593358559729	0.216229	0.6225	0.537359	0.268679
`Y(t-4)`	-0.341976205796012	0.173163	-1.9749	0.05558	0.02779
Productie	-0.0864265177172897	0.055892	-1.5463	0.130315	0.065158
M1	2.5704281506859	2.406703	1.068	0.292246	0.146123
M2	8.0452757771165	2.084308	3.8599	0.000427	0.000213
M3	10.6852562679373	2.782161	3.8406	0.000452	0.000226
M4	5.13454323216124	2.873556	1.7868	0.081945	0.040973
M5	-2.36138688814796	2.513384	-0.9395	0.353395	0.176698
M6	0.840375791480767	1.792159	0.4689	0.641807	0.320904
M7	3.94041195459863	2.04567	1.9262	0.061582	0.030791
M8	7.0899908939364	2.597087	2.73	0.009546	0.004773
M9	13.9240510104693	2.239463	6.2176	0	0
M10	0.826377650593013	2.851568	0.2898	0.773547	0.386773
M11	1.18103914539342	2.563276	0.4608	0.647601	0.323801
t	0.0648222506919648	0.095957	0.6755	0.503428	0.251714

Multiple Linear Regression - Regression Statistics
Multiple R	0.99638054568302
R-squared	0.992774191815591
Adjusted R-squared	0.989541593417303
F-TEST (value)	307.113371194316
F-TEST (DF numerator)	17
F-TEST (DF denominator)	38
p-value	0
Multiple Linear Regression - Residual Statistics
Residual Standard Deviation	2.03448320450095
Sum Squared Residuals	157.286632557065

Multiple Linear Regression - Actuals, Interpolation, and Residuals
Time or Index	Actuals	Interpolation Forecast	Residuals Prediction Error
1	86	83.6589070893564	2.34109291064364
2	86	85.9262057773954	0.0737942226046428
3	95.3	92.7238183292111	2.57618167078890
4	95.3	93.9446474661863	1.35535253381374
5	88.4	88.8237879072953	-0.423787907295282
6	86	86.7883049762286	-0.788304976228623
7	81.4	82.5658016669622	-1.16580166696223
8	83.7	81.3324346848708	2.36756531512918
9	95.3	90.7343274614483	4.56567253855169
10	88.4	89.8735256042379	-1.47352560423791
11	86	88.3118670445993	-2.31186704459934
12	83.7	83.4349840593609	0.265015940639098
13	76.7	78.8980886235964	-2.19808862359638
14	79.1	77.9224334885015	1.17756651149850
15	86	85.3700470387939	0.629952961206113
16	86	84.2136034806987	1.78639651930127
17	79.1	80.4388656745955	-1.33886567459555
18	76.7	77.2336878337599	-0.533687833759903
19	69.8	73.5985758205673	-3.79857582056726
20	69.8	70.3102532497208	-0.510253249720842
21	76.7	76.3357102100421	0.364289789957942
22	69.8	70.3968927995785	-0.596892799578531
23	67.4	66.8616840379591	0.538315962040915
24	65.1	65.1377577056107	-0.0377577056107264
25	58.1	60.0993434047856	-1.99934340478557
26	60.5	59.815100411429	0.684899588570984
27	65.1	67.1244315333738	-2.02443153337376
28	62.8	63.4290438873068	-0.629043887306756
29	55.8	57.3149884775548	-1.51498847755478
30	51.2	52.346582297977	-1.14658229797695
31	48.8	47.475393639148	1.32460636085203
32	48.8	49.0142227908515	-0.214222790851544
33	53.5	55.435213895826	-1.93521389582595
34	48.8	49.0007832636048	-0.200783263604812
35	46.5	45.5714430495826	0.928556950417436
36	44.2	43.8233230151309	0.376676984869109
37	39.5	40.0384940330097	-0.538494033009721
38	41.9	41.3728111235234	0.52718887647657
39	48.8	49.2002288447059	-0.400228844705945
40	46.5	47.9039321191682	-1.40393211916824
41	41.9	41.8062525572829	0.0937474427170518
42	39.5	38.9456307479733	0.554369252026719
43	37.2	36.529857880116	0.670142119884006
44	37.2	39.493317349177	-2.29331734917701
45	41.9	44.8947484326837	-2.99474843268369
46	39.5	37.2287983325787	2.27120166742125
47	39.5	38.655005867859	0.844994132140992
48	34.9	35.5039352198975	-0.603935219897477
49	34.9	32.5051668492520	2.39483315074803
50	34.9	37.3634491991507	-2.46344919915070
51	41.9	42.6814742539153	-0.781474253915302
52	41.9	43.00877304664	-1.10877304664000
53	39.5	36.3161053832714	3.18389461672855
54	39.5	37.5857941440612	1.91420585593875
55	41.9	38.9303709932065	2.96962900679346
56	46.5	45.8497719253798	0.650228074620219

Goldfeld-Quandt test for Heteroskedasticity
p-values	Alternative Hypothesis
breakpoint index	greater	2-sided	less
21	0.511403350885411	0.977193298229179	0.488596649114589
22	0.344657621482333	0.689315242964666	0.655342378517667
23	0.841910465743089	0.316179068513823	0.158089534256911
24	0.749249662393189	0.501500675213622	0.250750337606811
25	0.707882230510599	0.584235538978803	0.292117769489401
26	0.645280988208059	0.709438023583883	0.354719011791941
27	0.579009633017837	0.841980733964325	0.420990366982163
28	0.495760638547543	0.991521277095086	0.504239361452457
29	0.432083966257842	0.864167932515684	0.567916033742158
30	0.492270091696039	0.984540183392078	0.507729908303961
31	0.582569273483456	0.834861453033089	0.417430726516544
32	0.447762107908364	0.895524215816728	0.552237892091636
33	0.401742253161213	0.803484506322425	0.598257746838787
34	0.410191879457695	0.82038375891539	0.589808120542305
35	0.303597315841075	0.60719463168215	0.696402684158925

Meta Analysis of Goldfeld-Quandt test for Heteroskedasticity
Description	# significant tests	% significant tests	OK/NOK
1% type I error level	0	0	OK
5% type I error level	0	0	OK
10% type I error level	0	0	OK

Charts produced by software:

http://www.freestatistics.org/blog/date/2009/Dec/20/t12613076061whrt61i4saljbh/10n41y1261307442.png (opens in new window)

http://www.freestatistics.org/blog/date/2009/Dec/20/t12613076061whrt61i4saljbh/10n41y1261307442.ps (opens in new window)

Click here to open pdf file.

http://www.freestatistics.org/blog/date/2009/Dec/20/t12613076061whrt61i4saljbh/1pbec1261307442.png (opens in new window)

http://www.freestatistics.org/blog/date/2009/Dec/20/t12613076061whrt61i4saljbh/1pbec1261307442.ps (opens in new window)

Click here to open pdf file.

http://www.freestatistics.org/blog/date/2009/Dec/20/t12613076061whrt61i4saljbh/2iu6r1261307442.png (opens in new window)

http://www.freestatistics.org/blog/date/2009/Dec/20/t12613076061whrt61i4saljbh/2iu6r1261307442.ps (opens in new window)

Click here to open pdf file.

http://www.freestatistics.org/blog/date/2009/Dec/20/t12613076061whrt61i4saljbh/33xv91261307442.png (opens in new window)

http://www.freestatistics.org/blog/date/2009/Dec/20/t12613076061whrt61i4saljbh/33xv91261307442.ps (opens in new window)

Click here to open pdf file.

http://www.freestatistics.org/blog/date/2009/Dec/20/t12613076061whrt61i4saljbh/4h3so1261307442.png (opens in new window)

http://www.freestatistics.org/blog/date/2009/Dec/20/t12613076061whrt61i4saljbh/4h3so1261307442.ps (opens in new window)

Click here to open pdf file.

http://www.freestatistics.org/blog/date/2009/Dec/20/t12613076061whrt61i4saljbh/5jbu61261307442.png (opens in new window)

http://www.freestatistics.org/blog/date/2009/Dec/20/t12613076061whrt61i4saljbh/5jbu61261307442.ps (opens in new window)

Click here to open pdf file.

http://www.freestatistics.org/blog/date/2009/Dec/20/t12613076061whrt61i4saljbh/6jxa81261307442.png (opens in new window)

http://www.freestatistics.org/blog/date/2009/Dec/20/t12613076061whrt61i4saljbh/6jxa81261307442.ps (opens in new window)

Click here to open pdf file.

http://www.freestatistics.org/blog/date/2009/Dec/20/t12613076061whrt61i4saljbh/7dd761261307442.png (opens in new window)

http://www.freestatistics.org/blog/date/2009/Dec/20/t12613076061whrt61i4saljbh/7dd761261307442.ps (opens in new window)

Click here to open pdf file.

http://www.freestatistics.org/blog/date/2009/Dec/20/t12613076061whrt61i4saljbh/8idq81261307442.png (opens in new window)

http://www.freestatistics.org/blog/date/2009/Dec/20/t12613076061whrt61i4saljbh/8idq81261307442.ps (opens in new window)

Click here to open pdf file.

http://www.freestatistics.org/blog/date/2009/Dec/20/t12613076061whrt61i4saljbh/92o9i1261307442.png (opens in new window)

http://www.freestatistics.org/blog/date/2009/Dec/20/t12613076061whrt61i4saljbh/92o9i1261307442.ps (opens in new window)

Click here to open pdf file.

Parameters (Session):

par1 = 1 ; par2 = Include Monthly Dummies ; par3 = Linear Trend ;

Parameters (R input):

par1 = 1 ; par2 = Include Monthly Dummies ; par3 = Linear Trend ;

R code (references can be found in the software module):

library(lattice)
library(lmtest)
n25 <- 25 #minimum number of obs. for Goldfeld-Quandt test
par1 <- as.numeric(par1)
x <- t(y)
k <- length(x[1,])
n <- length(x[,1])
x1 <- cbind(x[,par1], x[,1:k!=par1])
mycolnames <- c(colnames(x)[par1], colnames(x)[1:k!=par1])
colnames(x1) <- mycolnames #colnames(x)[par1]
x <- x1
if (par3 == 'First Differences'){
x2 <- array(0, dim=c(n-1,k), dimnames=list(1:(n-1), paste('(1-B)',colnames(x),sep='')))
for (i in 1:n-1) {
for (j in 1:k) {
x2[i,j] <- x[i+1,j] - x[i,j]
}
}
x <- x2
}
if (par2 == 'Include Monthly Dummies'){
x2 <- array(0, dim=c(n,11), dimnames=list(1:n, paste('M', seq(1:11), sep ='')))
for (i in 1:11){
x2[seq(i,n,12),i] <- 1
}
x <- cbind(x, x2)
}
if (par2 == 'Include Quarterly Dummies'){
x2 <- array(0, dim=c(n,3), dimnames=list(1:n, paste('Q', seq(1:3), sep ='')))
for (i in 1:3){
x2[seq(i,n,4),i] <- 1
}
x <- cbind(x, x2)
}
k <- length(x[1,])
if (par3 == 'Linear Trend'){
x <- cbind(x, c(1:n))
colnames(x)[k+1] <- 't'
}
x
k <- length(x[1,])
df <- as.data.frame(x)
(mylm <- lm(df))
(mysum <- summary(mylm))
if (n > n25) {
kp3 <- k + 3
nmkm3 <- n - k - 3
gqarr <- array(NA, dim=c(nmkm3-kp3+1,3))
numgqtests <- 0
numsignificant1 <- 0
numsignificant5 <- 0
numsignificant10 <- 0
for (mypoint in kp3:nmkm3) {
j <- 0
numgqtests <- numgqtests + 1
for (myalt in c('greater', 'two.sided', 'less')) {
j <- j + 1
gqarr[mypoint-kp3+1,j] <- gqtest(mylm, point=mypoint, alternative=myalt)$p.value
}
if (gqarr[mypoint-kp3+1,2] < 0.01) numsignificant1 <- numsignificant1 + 1
if (gqarr[mypoint-kp3+1,2] < 0.05) numsignificant5 <- numsignificant5 + 1
if (gqarr[mypoint-kp3+1,2] < 0.10) numsignificant10 <- numsignificant10 + 1
}
gqarr
}
bitmap(file='test0.png')
plot(x[,1], type='l', main='Actuals and Interpolation', ylab='value of Actuals and Interpolation (dots)', xlab='time or index')
points(x[,1]-mysum$resid)
grid()
dev.off()
bitmap(file='test1.png')
plot(mysum$resid, type='b', pch=19, main='Residuals', ylab='value of Residuals', xlab='time or index')
grid()
dev.off()
bitmap(file='test2.png')
hist(mysum$resid, main='Residual Histogram', xlab='values of Residuals')
grid()
dev.off()
bitmap(file='test3.png')
densityplot(~mysum$resid,col='black',main='Residual Density Plot', xlab='values of Residuals')
dev.off()
bitmap(file='test4.png')
qqnorm(mysum$resid, main='Residual Normal Q-Q Plot')
qqline(mysum$resid)
grid()
dev.off()
(myerror <- as.ts(mysum$resid))
bitmap(file='test5.png')
dum <- cbind(lag(myerror,k=1),myerror)
dum
dum1 <- dum[2:length(myerror),]
dum1
z <- as.data.frame(dum1)
z
plot(z,main=paste('Residual Lag plot, lowess, and regression line'), ylab='values of Residuals', xlab='lagged values of Residuals')
lines(lowess(z))
abline(lm(z))
grid()
dev.off()
bitmap(file='test6.png')
acf(mysum$resid, lag.max=length(mysum$resid)/2, main='Residual Autocorrelation Function')
grid()
dev.off()
bitmap(file='test7.png')
pacf(mysum$resid, lag.max=length(mysum$resid)/2, main='Residual Partial Autocorrelation Function')
grid()
dev.off()
bitmap(file='test8.png')
opar <- par(mfrow = c(2,2), oma = c(0, 0, 1.1, 0))
plot(mylm, las = 1, sub='Residual Diagnostics')
par(opar)
dev.off()
if (n > n25) {
bitmap(file='test9.png')
plot(kp3:nmkm3,gqarr[,2], main='Goldfeld-Quandt test',ylab='2-sided p-value',xlab='breakpoint')
grid()
dev.off()
}
load(file='createtable')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a, 'Multiple Linear Regression - Estimated Regression Equation', 1, TRUE)
a<-table.row.end(a)
myeq <- colnames(x)[1]
myeq <- paste(myeq, '[t] = ', sep='')
for (i in 1:k){
if (mysum$coefficients[i,1] > 0) myeq <- paste(myeq, '+', '')
myeq <- paste(myeq, mysum$coefficients[i,1], sep=' ')
if (rownames(mysum$coefficients)[i] != '(Intercept)') {
myeq <- paste(myeq, rownames(mysum$coefficients)[i], sep='')
if (rownames(mysum$coefficients)[i] != 't') myeq <- paste(myeq, '[t]', sep='')
}
}
myeq <- paste(myeq, ' + e[t]')
a<-table.row.start(a)
a<-table.element(a, myeq)
a<-table.row.end(a)
a<-table.end(a)
table.save(a,file='mytable1.tab')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,hyperlink('http://www.xycoon.com/ols1.htm','Multiple Linear Regression - Ordinary Least Squares',''), 6, TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'Variable',header=TRUE)
a<-table.element(a,'Parameter',header=TRUE)
a<-table.element(a,'S.D.',header=TRUE)
a<-table.element(a,'T-STAT<br />H0: parameter = 0',header=TRUE)
a<-table.element(a,'2-tail p-value',header=TRUE)
a<-table.element(a,'1-tail p-value',header=TRUE)
a<-table.row.end(a)
for (i in 1:k){
a<-table.row.start(a)
a<-table.element(a,rownames(mysum$coefficients)[i],header=TRUE)
a<-table.element(a,mysum$coefficients[i,1])
a<-table.element(a, round(mysum$coefficients[i,2],6))
a<-table.element(a, round(mysum$coefficients[i,3],4))
a<-table.element(a, round(mysum$coefficients[i,4],6))
a<-table.element(a, round(mysum$coefficients[i,4]/2,6))
a<-table.row.end(a)
}
a<-table.end(a)
table.save(a,file='mytable2.tab')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a, 'Multiple Linear Regression - Regression Statistics', 2, TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'Multiple R',1,TRUE)
a<-table.element(a, sqrt(mysum$r.squared))
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'R-squared',1,TRUE)
a<-table.element(a, mysum$r.squared)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'Adjusted R-squared',1,TRUE)
a<-table.element(a, mysum$adj.r.squared)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'F-TEST (value)',1,TRUE)
a<-table.element(a, mysum$fstatistic[1])
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'F-TEST (DF numerator)',1,TRUE)
a<-table.element(a, mysum$fstatistic[2])
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'F-TEST (DF denominator)',1,TRUE)
a<-table.element(a, mysum$fstatistic[3])
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'p-value',1,TRUE)
a<-table.element(a, 1-pf(mysum$fstatistic[1],mysum$fstatistic[2],mysum$fstatistic[3]))
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'Multiple Linear Regression - Residual Statistics', 2, TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'Residual Standard Deviation',1,TRUE)
a<-table.element(a, mysum$sigma)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'Sum Squared Residuals',1,TRUE)
a<-table.element(a, sum(myerror*myerror))
a<-table.row.end(a)
a<-table.end(a)
table.save(a,file='mytable3.tab')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a, 'Multiple Linear Regression - Actuals, Interpolation, and Residuals', 4, TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'Time or Index', 1, TRUE)
a<-table.element(a, 'Actuals', 1, TRUE)
a<-table.element(a, 'Interpolation<br />Forecast', 1, TRUE)
a<-table.element(a, 'Residuals<br />Prediction Error', 1, TRUE)
a<-table.row.end(a)
for (i in 1:n) {
a<-table.row.start(a)
a<-table.element(a,i, 1, TRUE)
a<-table.element(a,x[i])
a<-table.element(a,x[i]-mysum$resid[i])
a<-table.element(a,mysum$resid[i])
a<-table.row.end(a)
}
a<-table.end(a)
table.save(a,file='mytable4.tab')
if (n > n25) {
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'Goldfeld-Quandt test for Heteroskedasticity',4,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'p-values',header=TRUE)
a<-table.element(a,'Alternative Hypothesis',3,header=TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'breakpoint index',header=TRUE)
a<-table.element(a,'greater',header=TRUE)
a<-table.element(a,'2-sided',header=TRUE)
a<-table.element(a,'less',header=TRUE)
a<-table.row.end(a)
for (mypoint in kp3:nmkm3) {
a<-table.row.start(a)
a<-table.element(a,mypoint,header=TRUE)
a<-table.element(a,gqarr[mypoint-kp3+1,1])
a<-table.element(a,gqarr[mypoint-kp3+1,2])
a<-table.element(a,gqarr[mypoint-kp3+1,3])
a<-table.row.end(a)
}
a<-table.end(a)
table.save(a,file='mytable5.tab')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'Meta Analysis of Goldfeld-Quandt test for Heteroskedasticity',4,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'Description',header=TRUE)
a<-table.element(a,'# significant tests',header=TRUE)
a<-table.element(a,'% significant tests',header=TRUE)
a<-table.element(a,'OK/NOK',header=TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'1% type I error level',header=TRUE)
a<-table.element(a,numsignificant1)
a<-table.element(a,numsignificant1/numgqtests)
if (numsignificant1/numgqtests < 0.01) dum <- 'OK' else dum <- 'NOK'
a<-table.element(a,dum)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'5% type I error level',header=TRUE)
a<-table.element(a,numsignificant5)
a<-table.element(a,numsignificant5/numgqtests)
if (numsignificant5/numgqtests < 0.05) dum <- 'OK' else dum <- 'NOK'
a<-table.element(a,dum)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'10% type I error level',header=TRUE)
a<-table.element(a,numsignificant10)
a<-table.element(a,numsignificant10/numgqtests)
if (numsignificant10/numgqtests < 0.1) dum <- 'OK' else dum <- 'NOK'
a<-table.element(a,dum)
a<-table.row.end(a)
a<-table.end(a)
table.save(a,file='mytable6.tab')
}