| | | *The author of this computation has been verified* | | R Software Module: /rwasp_multipleregression.wasp (opens new window with default values) | | Title produced by software: Multiple Regression | | Date of computation: Sun, 21 Nov 2010 09:32:48 +0000 | | | | Cite this page as follows: | | Statistical Computations at FreeStatistics.org, Office for Research Development and Education, URL http://www.freestatistics.org/blog/date/2010/Nov/21/t1290332008tm0mnol5qep763b.htm/, Retrieved Sun, 21 Nov 2010 10:33:31 +0100 | | | | BibTeX entries for LaTeX users: | @Manual{KEY,
author = {{YOUR NAME}},
publisher = {Office for Research Development and Education},
title = {Statistical Computations at FreeStatistics.org, URL http://www.freestatistics.org/blog/date/2010/Nov/21/t1290332008tm0mnol5qep763b.htm/},
year = {2010},
}
@Manual{R,
title = {R: A Language and Environment for Statistical Computing},
author = {{R Development Core Team}},
organization = {R Foundation for Statistical Computing},
address = {Vienna, Austria},
year = {2010},
note = {{ISBN} 3-900051-07-0},
url = {http://www.R-project.org},
}
| | | | Original text written by user: | | | | | IsPrivate? | | No (this computation is public) | | | | User-defined keywords: | | | | | Dataseries X: | | » Textbox « » Textfile « » CSV « | | 24 14 11 12 24 26
25 11 7 8 25 23
17 6 17 8 30 25
18 12 10 8 19 23
18 8 12 9 22 19
16 10 12 7 22 29
20 10 11 4 25 25
16 11 11 11 23 21
18 16 12 7 17 22
17 11 13 7 21 25
23 13 14 12 19 24
30 12 16 10 19 18
23 8 11 10 15 22
18 12 10 8 16 15
15 11 11 8 23 22
12 4 15 4 27 28
21 9 9 9 22 20
15 8 11 8 14 12
20 8 17 7 22 24
31 14 17 11 23 20
27 15 11 9 23 21
34 16 18 11 21 20
21 9 14 13 19 21
31 14 10 8 18 23
19 11 11 8 20 28
16 8 15 9 23 24
20 9 15 6 25 24
21 9 13 9 19 24
22 9 16 9 24 23
17 9 13 6 22 23
24 10 9 6 25 29
25 16 18 16 26 24
26 11 18 5 29 18
25 8 12 7 32 25
17 9 17 9 25 21
32 16 9 6 29 26
33 11 9 6 28 22
13 16 12 5 17 22
32 12 18 12 28 22
25 12 12 7 29 23
29 14 18 10 26 30
22 9 14 9 25 23
18 10 15 8 14 17
17 9 16 5 25 23
20 10 10 8 26 23
15 12 11 8 20 25
20 14 14 10 18 24
33 14 9 6 32 24
29 10 12 8 25 23
23 14 17 7 25 21
26 16 5 4 23 24
18 9 12 8 21 24
20 10 12 8 20 28
11 6 6 4 15 16
28 8 24 20 30 20
26 13 12 8 24 29
22 10 12 8 26 27
17 8 14 6 24 etc... | | | | Output produced by software: | Enter (or paste) a matrix (table) containing all data (time) series. Every column represents a different variable and must be delimited by a space or Tab. Every row represents a period in time (or category) and must be delimited by hard returns. The easiest way to enter data is to copy and paste a block of spreadsheet cells. Please, do not use commas or spaces to seperate groups of digits!
| Multiple Linear Regression - Estimated Regression Equation | | CM[t] = -1.97155708164813 + 0.810124516285502D[t] + 0.251253601241107PE[t] + 0.188518804715737PC[t] + 0.566064813317673PS[t] -0.115718741599822O[t] + e[t] |
| Multiple Linear Regression - Ordinary Least Squares | | Variable | Parameter | S.D. | T-STAT
H0: parameter = 0 | 2-tail p-value | 1-tail p-value | | (Intercept) | -1.97155708164813 | 3.052906 | -0.6458 | 0.519378 | 0.259689 | | D | 0.810124516285502 | 0.130335 | 6.2157 | 0 | 0 | | PE | 0.251253601241107 | 0.13276 | 1.8925 | 0.060307 | 0.030154 | | PC | 0.188518804715737 | 0.168259 | 1.1204 | 0.264294 | 0.132147 | | PS | 0.566064813317673 | 0.095813 | 5.908 | 0 | 0 | | O | -0.115718741599822 | 0.103024 | -1.1232 | 0.263103 | 0.131551 |
| Multiple Linear Regression - Regression Statistics | | Multiple R | 0.638102890589065 | | R-squared | 0.40717529897812 | | Adjusted R-squared | 0.387801942735575 | | F-TEST (value) | 21.0172823893021 | | F-TEST (DF numerator) | 5 | | F-TEST (DF denominator) | 153 | | p-value | 5.55111512312578e-16 | | Multiple Linear Regression - Residual Statistics | | Residual Standard Deviation | 4.47771018087769 | | Sum Squared Residuals | 3067.63293498216 |
| Multiple Linear Regression - Actuals, Interpolation, and Residuals | | Time or Index | Actuals | Interpolation
Forecast | Residuals
Prediction Error | | 1 | 24 | 24.9730696546186 | -0.973069654618646 | | 2 | 25 | 21.6968275200519 | 3.30317247994806 | | 3 | 17 | 22.7576275344242 | -5.75762753442423 | | 4 | 18 | 19.8643239601547 | -1.86432396015473 | | 5 | 18 | 19.475921308563 | -1.47592130856298 | | 6 | 16 | 19.5619453157043 | -3.56194531570428 | | 7 | 20 | 20.9062047066683 | -0.906204706668275 | | 8 | 16 | 22.3667061957279 | -6.36670619572788 | | 9 | 18 | 22.4023995380277 | -4.40239953802769 | | 10 | 17 | 20.5201335863125 | -3.52013358631251 | | 11 | 23 | 22.3178193586678 | 0.682180641332218 | | 12 | 30 | 22.327476885032 | 7.67252311496805 | | 13 | 23 | 15.1035765940144 | 7.89642340598557 | | 14 | 18 | 19.0918794530003 | -1.09187945300029 | | 15 | 15 | 21.6854310399808 | -6.68543103998085 | | 16 | 12 | 17.8354454157556 | -5.83544541575557 | | 17 | 21 | 19.4165662795253 | 1.58343372047466 | | 18 | 15 | 15.3176615872635 | -0.317661587263507 | | 19 | 20 | 19.7765579973379 | 0.223442002662073 | | 20 | 31 | 26.4203200936308 | 4.57967990636915 | | 21 | 27 | 25.2301666514384 | 1.76983334856159 | | 22 | 34 | 27.1596931008076 | 6.84030689919238 | | 23 | 21 | 19.612996323041 | 1.38700367695902 | | 24 | 31 | 20.9185081794081 | 10.0814918205919 | | 25 | 19 | 19.2929241504289 | -0.292924150428893 | | 26 | 16 | 20.2171532176049 | -4.21715321760486 | | 27 | 20 | 21.5938509463785 | -1.5938509463785 | | 28 | 21 | 18.2605112781375 | 2.73948872186254 | | 29 | 22 | 21.960314890049 | 0.039685109951034 | | 30 | 17 | 19.5088680455431 | -2.50886804554309 | | 31 | 24 | 20.3178601472182 | 3.68213985278175 | | 32 | 25 | 30.4697362245754 | -5.46973622457538 | | 33 | 26 | 26.7379136808267 | -0.737913680826711 | | 34 | 25 | 24.0652193827093 | 0.934780617290694 | | 35 | 17 | 23.0090707878074 | -6.00907078780739 | | 36 | 32 | 27.7900227230014 | 4.20997727699858 | | 37 | 33 | 23.6362102946555 | 9.36378970534447 | | 38 | 13 | 22.0253619285962 | -9.02536192859621 | | 39 | 32 | 27.8387300504054 | 4.16126994959459 | | 40 | 25 | 25.8389604910979 | -0.838960491097936 | | 41 | 29 | 27.024061914111 | 1.97593808588899 | | 42 | 22 | 22.0238725008844 | -0.0238725008844258 | | 43 | 18 | 17.3643313167998 | 0.635668683200175 | | 44 | 17 | 21.7723044845037 | -4.77230448450369 | | 45 | 20 | 22.2065286208074 | -2.20652862080744 | | 46 | 15 | 20.4502048915139 | -5.45020489151386 | | 47 | 20 | 22.1848414522041 | -2.18484145220414 | | 48 | 33 | 28.0994056135831 | 4.90059438641692 | | 49 | 29 | 22.142971009972 | 6.85702899002802 | | 50 | 23 | 26.6826557598034 | -3.68265575980342 | | 51 | 26 | 23.2430193118991 | 2.75698068810088 | | 52 | 18 | 18.952868498816 | -0.95286849881596 | | 53 | 20 | 18.7340532353845 | 1.2659467646155 | | 54 | 11 | 11.7902591765424 | -0.790259176542405 | | 55 | 28 | 28.9774711402709 | -0.977471140270937 | | 56 | 26 | 23.3129672959119 | 2.68703270408813 | | 57 | 22 | 22.2461608568904 | -0.24616085689036 | | 58 | 17 | 20.1978454987339 | -3.19784549873386 | | 59 | 12 | 15.4254660880949 | -3.42546608809486 | | 60 | 14 | 21.0281654373449 | -7.02816543734494 | | 61 | 17 | 20.7238630018849 | -3.72386300188489 | | 62 | 21 | 21.3354034468641 | -0.335403446864113 | | 63 | 19 | 22.9325499189927 | -3.93254991899267 | | 64 | 18 | 23.0750654036623 | -5.0750654036623 | | 65 | 10 | 17.9297721146776 | -7.92977211467762 | | 66 | 29 | 24.2201359970942 | 4.77986400290577 | | 67 | 31 | 18.457555194607 | 12.542444805393 | | 68 | 19 | 22.9476672047626 | -3.94766720476257 | | 69 | 9 | 20.0659733838091 | -11.0659733838091 | | 70 | 20 | 22.4704044418167 | -2.47040444181673 | | 71 | 28 | 17.6195978476967 | 10.3804021523033 | | 72 | 19 | 18.1263076319767 | 0.873692368023276 | | 73 | 30 | 23.0600995039614 | 6.93990049603859 | | 74 | 29 | 27.134541986358 | 1.86545801364201 | | 75 | 26 | 21.4781322047787 | 4.52186779522132 | | 76 | 23 | 19.5440844265833 | 3.45591557341674 | | 77 | 13 | 22.7619883304533 | -9.76198833045328 | | 78 | 21 | 22.6403328681881 | -1.64033286818809 | | 79 | 19 | 21.4342707638265 | -2.43427076382649 | | 80 | 28 | 22.9430302596669 | 5.05696974033307 | | 81 | 23 | 25.5488853193873 | -2.54888531938727 | | 82 | 18 | 13.775544612248 | 4.22445538775199 | | 83 | 21 | 20.7338035054779 | 0.266196494522131 | | 84 | 20 | 21.7890552501971 | -1.78905525019705 | | 85 | 23 | 19.953634409697 | 3.04636559030299 | | 86 | 21 | 20.823548318318 | 0.176451681682022 | | 87 | 21 | 21.7765070663015 | -0.776507066301508 | | 88 | 15 | 22.8032661951564 | -7.80326619515638 | | 89 | 28 | 27.147195644037 | 0.852804355962999 | | 90 | 19 | 17.6573711819145 | 1.3426288180855 | | 91 | 26 | 21.241739029455 | 4.75826097054501 | | 92 | 10 | 13.1981887926427 | -3.1981887926427 | | 93 | 16 | 17.1052598018456 | -1.10525980184556 | | 94 | 22 | 21.1686559891103 | 0.831344010889731 | | 95 | 19 | 18.7314962822069 | 0.26850371779314 | | 96 | 31 | 28.7736261084291 | 2.22637389157087 | | 97 | 31 | 25.1990473784126 | 5.8009526215874 | | 98 | 29 | 24.802119615067 | 4.19788038493298 | | 99 | 19 | 17.4133114789467 | 1.58668852105333 | | 100 | 22 | 18.8946458843887 | 3.10535411561134 | | 101 | 23 | 22.3730772796911 | 0.62692272030893 | | 102 | 15 | 16.1706084549776 | -1.1706084549776 | | 103 | 20 | 21.4483664364161 | -1.44836643641609 | | 104 | 18 | 19.5049798788849 | -1.5049798788849 | | 105 | 23 | 21.9846165671171 | 1.01538343288295 | | 106 | 25 | 20.9638904859829 | 4.03610951401714 | | 107 | 21 | 16.5635547265782 | 4.43644527342175 | | 108 | 24 | 19.4904987572516 | 4.5095012427484 | | 109 | 25 | 25.2360293362311 | -0.23602933623114 | | 110 | 17 | 19.5772208157054 | -2.57722081570542 | | 111 | 13 | 14.5703651925901 | -1.57036519259012 | | 112 | 28 | 18.2036391664048 | 9.79636083359519 | | 113 | 21 | 20.1156089993067 | 0.884391000693341 | | 114 | 25 | 28.140636065485 | -3.14063606548499 | | 115 | 9 | 20.7272742072834 | -11.7272742072834 | | 116 | 16 | 17.8284411696244 | -1.82844116962435 | | 117 | 19 | 21.2002096254339 | -2.2002096254339 | | 118 | 17 | 19.4548480129136 | -2.45484801291361 | | 119 | 25 | 24.5118355020002 | 0.488164497999802 | | 120 | 20 | 15.5584155586162 | 4.44158444138375 | | 121 | 29 | 21.6245358561065 | 7.37546414389351 | | 122 | 14 | 19.0460894061991 | -5.04608940619911 | | 123 | 22 | 26.9144076581427 | -4.9144076581427 | | 124 | 15 | 15.5764012107348 | -0.576401210734847 | | 125 | 19 | 25.4228566000411 | -6.42285660004114 | | 126 | 20 | 21.9451042791923 | -1.94510427919232 | | 127 | 15 | 17.452226374503 | -2.45222637450297 | | 128 | 20 | 21.7886208868992 | -1.78862088689923 | | 129 | 18 | 20.2225815390998 | -2.22258153909977 | | 130 | 33 | 25.4668428039909 | 7.5331571960091 | | 131 | 22 | 23.7824344363272 | -1.78243443632724 | | 132 | 16 | 16.4697006570271 | -0.46970065702706 | | 133 | 17 | 19.0367506268633 | -2.03675062686334 | | 134 | 16 | 15.052432261591 | 0.94756773840901 | | 135 | 21 | 17.0483876901129 | 3.95161230988708 | | 136 | 26 | 27.6421945331063 | -1.64219453310631 | | 137 | 18 | 21.1470742942904 | -3.14707429429043 | | 138 | 18 | 23.0959206112274 | -5.09592061122736 | | 139 | 17 | 18.3312627872462 | -1.33126278724619 | | 140 | 22 | 24.7434940752527 | -2.74349407525273 | | 141 | 30 | 24.7275661238695 | 5.27243387613054 | | 142 | 30 | 27.2739964505683 | 2.72600354943171 | | 143 | 24 | 29.9008223341231 | -5.90082233412311 | | 144 | 21 | 21.9917911761762 | -0.991791176176224 | | 145 | 21 | 25.3787580941457 | -4.3787580941457 | | 146 | 29 | 27.3918377820479 | 1.60816221795207 | | 147 | 31 | 23.240508271007 | 7.75949172899296 | | 148 | 20 | 18.9759710592584 | 1.0240289407416 | | 149 | 16 | 14.1875805146353 | 1.81241948536466 | | 150 | 22 | 18.9190989475258 | 3.08090105247424 | | 151 | 20 | 20.3316462195076 | -0.331646219507597 | | 152 | 28 | 27.3269489577319 | 0.673051042268083 | | 153 | 38 | 26.5958059363835 | 11.4041940636165 | | 154 | 22 | 19.3348333644292 | 2.66516663557078 | | 155 | 20 | 25.6868097712468 | -5.68680977124681 | | 156 | 17 | 18.0421110887897 | -1.04211108878971 | | 157 | 28 | 24.4504319189554 | 3.54956808104462 | | 158 | 22 | 24.1216672736301 | -2.12166727363008 | | 159 | 31 | 26.0892814723567 | 4.91071852764329 |
| Goldfeld-Quandt test for Heteroskedasticity | | p-values | Alternative Hypothesis | | breakpoint index | greater | 2-sided | less | | 9 | 0.211396023302327 | 0.422792046604655 | 0.788603976697673 | | 10 | 0.102076375342588 | 0.204152750685175 | 0.897923624657412 | | 11 | 0.227238038192075 | 0.454476076384149 | 0.772761961807925 | | 12 | 0.651688236191951 | 0.696623527616098 | 0.348311763808049 | | 13 | 0.667307232542331 | 0.665385534915338 | 0.332692767457669 | | 14 | 0.642015414981076 | 0.715969170037848 | 0.357984585018924 | | 15 | 0.647421329942229 | 0.705157340115542 | 0.352578670057771 | | 16 | 0.58200717018021 | 0.83598565963958 | 0.41799282981979 | | 17 | 0.497441679833797 | 0.994883359667594 | 0.502558320166203 | | 18 | 0.466853717517482 | 0.933707435034964 | 0.533146282482518 | | 19 | 0.40318515945476 | 0.80637031890952 | 0.59681484054524 | | 20 | 0.437609217255157 | 0.875218434510315 | 0.562390782744843 | | 21 | 0.39690152509777 | 0.79380305019554 | 0.60309847490223 | | 22 | 0.400777969653793 | 0.801555939307585 | 0.599222030346207 | | 23 | 0.338769951631692 | 0.677539903263385 | 0.661230048368308 | | 24 | 0.603341567728286 | 0.793316864543429 | 0.396658432271714 | | 25 | 0.53355120104486 | 0.932897597910281 | 0.46644879895514 | | 26 | 0.503544024150427 | 0.992911951699147 | 0.496455975849573 | | 27 | 0.441730998369871 | 0.883461996739741 | 0.558269001630129 | | 28 | 0.395183167548785 | 0.79036633509757 | 0.604816832451215 | | 29 | 0.334977520412384 | 0.669955040824767 | 0.665022479587616 | | 30 | 0.282918967778749 | 0.565837935557497 | 0.717081032221252 | | 31 | 0.342901815128517 | 0.685803630257034 | 0.657098184871483 | | 32 | 0.404232070072038 | 0.808464140144076 | 0.595767929927962 | | 33 | 0.360398880532785 | 0.72079776106557 | 0.639601119467215 | | 34 | 0.370631372835848 | 0.741262745671697 | 0.629368627164152 | | 35 | 0.385307154342616 | 0.770614308685231 | 0.614692845657384 | | 36 | 0.375949698359978 | 0.751899396719955 | 0.624050301640022 | | 37 | 0.554989703390057 | 0.890020593219885 | 0.445010296609942 | | 38 | 0.758465746223827 | 0.483068507552346 | 0.241534253776173 | | 39 | 0.754517941616512 | 0.490964116766976 | 0.245482058383488 | | 40 | 0.712620047429136 | 0.574759905141728 | 0.287379952570864 | | 41 | 0.68761372332183 | 0.62477255335634 | 0.31238627667817 | | 42 | 0.638173577653739 | 0.723652844692523 | 0.361826422346261 | | 43 | 0.589575343770854 | 0.820849312458293 | 0.410424656229147 | | 44 | 0.57618726679963 | 0.84762546640074 | 0.42381273320037 | | 45 | 0.541737547166 | 0.916524905668 | 0.458262452834 | | 46 | 0.56383048884673 | 0.87233902230654 | 0.43616951115327 | | 47 | 0.522810428163516 | 0.954379143672968 | 0.477189571836484 | | 48 | 0.513226336040152 | 0.973547327919696 | 0.486773663959848 | | 49 | 0.578119098257291 | 0.843761803485418 | 0.421880901742709 | | 50 | 0.557204565171353 | 0.885590869657294 | 0.442795434828647 | | 51 | 0.521832610252995 | 0.95633477949401 | 0.478167389747005 | | 52 | 0.472518698692183 | 0.945037397384367 | 0.527481301307816 | | 53 | 0.434388024384904 | 0.868776048769809 | 0.565611975615096 | | 54 | 0.387597441853448 | 0.775194883706895 | 0.612402558146552 | | 55 | 0.344799433006013 | 0.689598866012025 | 0.655200566993987 | | 56 | 0.31767947265381 | 0.63535894530762 | 0.68232052734619 | | 57 | 0.274752158603492 | 0.549504317206985 | 0.725247841396508 | | 58 | 0.251105924453974 | 0.502211848907948 | 0.748894075546026 | | 59 | 0.231434319721369 | 0.462868639442737 | 0.768565680278631 | | 60 | 0.290144078219361 | 0.580288156438723 | 0.709855921780639 | | 61 | 0.278497186524718 | 0.556994373049437 | 0.721502813475282 | | 62 | 0.241248961424153 | 0.482497922848306 | 0.758751038575847 | | 63 | 0.228675123650196 | 0.457350247300393 | 0.771324876349804 | | 64 | 0.262536263897205 | 0.52507252779441 | 0.737463736102795 | | 65 | 0.338838414452532 | 0.677676828905065 | 0.661161585547468 | | 66 | 0.341559278538761 | 0.683118557077522 | 0.658440721461239 | | 67 | 0.67452621767385 | 0.650947564652299 | 0.325473782326149 | | 68 | 0.667298147675611 | 0.665403704648777 | 0.332701852324389 | | 69 | 0.844206840041378 | 0.311586319917243 | 0.155793159958622 | | 70 | 0.82447818917953 | 0.35104362164094 | 0.17552181082047 | | 71 | 0.930528498621507 | 0.138943002756987 | 0.0694715013784935 | | 72 | 0.914237531913636 | 0.171524936172728 | 0.0857624680863639 | | 73 | 0.937422576584964 | 0.125154846830072 | 0.0625774234150359 | | 74 | 0.92557432123351 | 0.148851357532979 | 0.0744256787664894 | | 75 | 0.927322042553002 | 0.145355914893997 | 0.0726779574469984 | | 76 | 0.921002404447875 | 0.15799519110425 | 0.078997595552125 | | 77 | 0.97009612299005 | 0.059807754019899 | 0.0299038770099495 | | 78 | 0.962737123434992 | 0.0745257531300151 | 0.0372628765650076 | | 79 | 0.955322112720419 | 0.0893557745591622 | 0.0446778872795811 | | 80 | 0.958001069235287 | 0.0839978615294255 | 0.0419989307647127 | | 81 | 0.950327240193387 | 0.0993455196132268 | 0.0496727598066134 | | 82 | 0.950009769558878 | 0.0999804608822439 | 0.0499902304411219 | | 83 | 0.937189377311647 | 0.125621245376706 | 0.0628106226883528 | | 84 | 0.924429516664979 | 0.151140966670042 | 0.0755704833350211 | | 85 | 0.915951672892238 | 0.168096654215525 | 0.0840483271077623 | | 86 | 0.900653181134239 | 0.198693637731522 | 0.0993468188657611 | | 87 | 0.879710042132296 | 0.240579915735408 | 0.120289957867704 | | 88 | 0.923727400022814 | 0.152545199954373 | 0.0762725999771865 | | 89 | 0.907794947977105 | 0.184410104045791 | 0.0922050520228953 | | 90 | 0.88852102833551 | 0.222957943328979 | 0.11147897166449 | | 91 | 0.890348508172257 | 0.219302983655487 | 0.109651491827743 | | 92 | 0.87972329404173 | 0.240553411916539 | 0.12027670595827 | | 93 | 0.858486388567674 | 0.283027222864652 | 0.141513611432326 | | 94 | 0.83180233324056 | 0.336395333518881 | 0.168197666759441 | | 95 | 0.799891741151273 | 0.400216517697453 | 0.200108258848727 | | 96 | 0.771363589009715 | 0.45727282198057 | 0.228636410990285 | | 97 | 0.790445706797612 | 0.419108586404776 | 0.209554293202388 | | 98 | 0.785253416561085 | 0.429493166877829 | 0.214746583438915 | | 99 | 0.751315699297826 | 0.497368601404349 | 0.248684300702174 | | 100 | 0.727772355364809 | 0.544455289270383 | 0.272227644635191 | | 101 | 0.686415862962309 | 0.627168274075382 | 0.313584137037691 | | 102 | 0.648669584234022 | 0.702660831531956 | 0.351330415765978 | | 103 | 0.610688735942807 | 0.778622528114387 | 0.389311264057193 | | 104 | 0.568912513183682 | 0.862174973632637 | 0.431087486816318 | | 105 | 0.523348261113884 | 0.953303477772232 | 0.476651738886116 | | 106 | 0.50374480286819 | 0.99251039426362 | 0.49625519713181 | | 107 | 0.500601496808818 | 0.998797006382364 | 0.499398503191182 | | 108 | 0.512066888836196 | 0.975866222327607 | 0.487933111163804 | | 109 | 0.461970607190606 | 0.923941214381212 | 0.538029392809394 | | 110 | 0.438871952745131 | 0.877743905490262 | 0.561128047254869 | | 111 | 0.399245111949125 | 0.79849022389825 | 0.600754888050876 | | 112 | 0.622464003183592 | 0.755071993632816 | 0.377535996816408 | | 113 | 0.6143504316766 | 0.7712991366468 | 0.3856495683234 | | 114 | 0.586012234060728 | 0.827975531878544 | 0.413987765939272 | | 115 | 0.787995057379245 | 0.424009885241511 | 0.212004942620755 | | 116 | 0.766002840747051 | 0.467994318505898 | 0.233997159252949 | | 117 | 0.755053282831569 | 0.489893434336863 | 0.244946717168431 | | 118 | 0.728310027616058 | 0.543379944767885 | 0.271689972383942 | | 119 | 0.680521723246862 | 0.638956553506276 | 0.319478276753138 | | 120 | 0.689821686952418 | 0.620356626095164 | 0.310178313047582 | | 121 | 0.741250456736066 | 0.517499086527867 | 0.258749543263934 | | 122 | 0.746311092056203 | 0.507377815887594 | 0.253688907943797 | | 123 | 0.752066455515674 | 0.495867088968652 | 0.247933544484326 | | 124 | 0.702722865924083 | 0.594554268151834 | 0.297277134075917 | | 125 | 0.746671936072011 | 0.506656127855978 | 0.253328063927989 | | 126 | 0.719710175859793 | 0.560579648280415 | 0.280289824140207 | | 127 | 0.709720699392158 | 0.580558601215684 | 0.290279300607842 | | 128 | 0.676029679145159 | 0.647940641709682 | 0.323970320854841 | | 129 | 0.650880955155709 | 0.698238089688582 | 0.349119044844291 | | 130 | 0.72046223026605 | 0.559075539467901 | 0.27953776973395 | | 131 | 0.666986057099335 | 0.66602788580133 | 0.333013942900665 | | 132 | 0.606230214360545 | 0.78753957127891 | 0.393769785639455 | | 133 | 0.605895172509634 | 0.788209654980733 | 0.394104827490366 | | 134 | 0.546964777920311 | 0.906070444159378 | 0.453035222079689 | | 135 | 0.506212479145598 | 0.987575041708803 | 0.493787520854402 | | 136 | 0.478869778858994 | 0.957739557717987 | 0.521130221141006 | | 137 | 0.485143350871994 | 0.970286701743989 | 0.514856649128006 | | 138 | 0.528733486885151 | 0.9425330262297 | 0.47126651311485 | | 139 | 0.46164830027676 | 0.923296600553519 | 0.53835169972324 | | 140 | 0.387508920972158 | 0.775017841944315 | 0.612491079027842 | | 141 | 0.500398992333827 | 0.999202015332345 | 0.499601007666173 | | 142 | 0.447731430106021 | 0.895462860212042 | 0.552268569893979 | | 143 | 0.377989760724786 | 0.755979521449573 | 0.622010239275214 | | 144 | 0.298009846375371 | 0.596019692750742 | 0.701990153624629 | | 145 | 0.355263275293376 | 0.710526550586751 | 0.644736724706624 | | 146 | 0.262950876609858 | 0.525901753219716 | 0.737049123390142 | | 147 | 0.340573335736029 | 0.681146671472058 | 0.659426664263971 | | 148 | 0.234921271540772 | 0.469842543081545 | 0.765078728459228 | | 149 | 0.146077973504984 | 0.292155947009969 | 0.853922026495016 | | 150 | 0.0919194134704893 | 0.183838826940979 | 0.90808058652951 |
| Meta Analysis of Goldfeld-Quandt test for Heteroskedasticity | | Description | # significant tests | % significant tests | OK/NOK | | 1% type I error level | 0 | 0 | OK | | 5% type I error level | 0 | 0 | OK | | 10% type I error level | 6 | 0.0422535211267606 | OK |
| | | | Charts produced by software: |  | | http://www.freestatistics.org/blog/date/2010/Nov/21/t1290332008tm0mnol5qep763b/107gb31290331955.png (open in new window) | | http://www.freestatistics.org/blog/date/2010/Nov/21/t1290332008tm0mnol5qep763b/107gb31290331955.ps (open in new window) |
 | | http://www.freestatistics.org/blog/date/2010/Nov/21/t1290332008tm0mnol5qep763b/185bw1290331954.png (open in new window) | | http://www.freestatistics.org/blog/date/2010/Nov/21/t1290332008tm0mnol5qep763b/185bw1290331954.ps (open in new window) |
 | | http://www.freestatistics.org/blog/date/2010/Nov/21/t1290332008tm0mnol5qep763b/2jfah1290331954.png (open in new window) | | http://www.freestatistics.org/blog/date/2010/Nov/21/t1290332008tm0mnol5qep763b/2jfah1290331954.ps (open in new window) |
 | | http://www.freestatistics.org/blog/date/2010/Nov/21/t1290332008tm0mnol5qep763b/3jfah1290331954.png (open in new window) | | http://www.freestatistics.org/blog/date/2010/Nov/21/t1290332008tm0mnol5qep763b/3jfah1290331954.ps (open in new window) |
 | | http://www.freestatistics.org/blog/date/2010/Nov/21/t1290332008tm0mnol5qep763b/4jfah1290331954.png (open in new window) | | http://www.freestatistics.org/blog/date/2010/Nov/21/t1290332008tm0mnol5qep763b/4jfah1290331954.ps (open in new window) |
 | | http://www.freestatistics.org/blog/date/2010/Nov/21/t1290332008tm0mnol5qep763b/5jfah1290331954.png (open in new window) | | http://www.freestatistics.org/blog/date/2010/Nov/21/t1290332008tm0mnol5qep763b/5jfah1290331954.ps (open in new window) |
 | | http://www.freestatistics.org/blog/date/2010/Nov/21/t1290332008tm0mnol5qep763b/6uoa21290331954.png (open in new window) | | http://www.freestatistics.org/blog/date/2010/Nov/21/t1290332008tm0mnol5qep763b/6uoa21290331954.ps (open in new window) |
 | | http://www.freestatistics.org/blog/date/2010/Nov/21/t1290332008tm0mnol5qep763b/74xq51290331954.png (open in new window) | | http://www.freestatistics.org/blog/date/2010/Nov/21/t1290332008tm0mnol5qep763b/74xq51290331954.ps (open in new window) |
 | | http://www.freestatistics.org/blog/date/2010/Nov/21/t1290332008tm0mnol5qep763b/84xq51290331954.png (open in new window) | | http://www.freestatistics.org/blog/date/2010/Nov/21/t1290332008tm0mnol5qep763b/84xq51290331954.ps (open in new window) |
 | | http://www.freestatistics.org/blog/date/2010/Nov/21/t1290332008tm0mnol5qep763b/94xq51290331954.png (open in new window) | | http://www.freestatistics.org/blog/date/2010/Nov/21/t1290332008tm0mnol5qep763b/94xq51290331954.ps (open in new window) |
| | | | Parameters (Session): | | par1 = 1 ; par2 = Do not include Seasonal Dummies ; par3 = No Linear Trend ; | | | | Parameters (R input): | | par1 = 1 ; par2 = Do not include Seasonal Dummies ; par3 = No Linear Trend ; | | | | R code (references can be found in the software module): | library(lattice)
library(lmtest)
n25 <- 25 #minimum number of obs. for Goldfeld-Quandt test
par1 <- as.numeric(par1)
x <- t(y)
k <- length(x[1,])
n <- length(x[,1])
x1 <- cbind(x[,par1], x[,1:k!=par1])
mycolnames <- c(colnames(x)[par1], colnames(x)[1:k!=par1])
colnames(x1) <- mycolnames #colnames(x)[par1]
x <- x1
if (par3 == 'First Differences'){
x2 <- array(0, dim=c(n-1,k), dimnames=list(1:(n-1), paste('(1-B)',colnames(x),sep='')))
for (i in 1:n-1) {
for (j in 1:k) {
x2[i,j] <- x[i+1,j] - x[i,j]
}
}
x <- x2
}
if (par2 == 'Include Monthly Dummies'){
x2 <- array(0, dim=c(n,11), dimnames=list(1:n, paste('M', seq(1:11), sep ='')))
for (i in 1:11){
x2[seq(i,n,12),i] <- 1
}
x <- cbind(x, x2)
}
if (par2 == 'Include Quarterly Dummies'){
x2 <- array(0, dim=c(n,3), dimnames=list(1:n, paste('Q', seq(1:3), sep ='')))
for (i in 1:3){
x2[seq(i,n,4),i] <- 1
}
x <- cbind(x, x2)
}
k <- length(x[1,])
if (par3 == 'Linear Trend'){
x <- cbind(x, c(1:n))
colnames(x)[k+1] <- 't'
}
x
k <- length(x[1,])
df <- as.data.frame(x)
(mylm <- lm(df))
(mysum <- summary(mylm))
if (n > n25) {
kp3 <- k + 3
nmkm3 <- n - k - 3
gqarr <- array(NA, dim=c(nmkm3-kp3+1,3))
numgqtests <- 0
numsignificant1 <- 0
numsignificant5 <- 0
numsignificant10 <- 0
for (mypoint in kp3:nmkm3) {
j <- 0
numgqtests <- numgqtests + 1
for (myalt in c('greater', 'two.sided', 'less')) {
j <- j + 1
gqarr[mypoint-kp3+1,j] <- gqtest(mylm, point=mypoint, alternative=myalt)$p.value
}
if (gqarr[mypoint-kp3+1,2] < 0.01) numsignificant1 <- numsignificant1 + 1
if (gqarr[mypoint-kp3+1,2] < 0.05) numsignificant5 <- numsignificant5 + 1
if (gqarr[mypoint-kp3+1,2] < 0.10) numsignificant10 <- numsignificant10 + 1
}
gqarr
}
bitmap(file='test0.png')
plot(x[,1], type='l', main='Actuals and Interpolation', ylab='value of Actuals and Interpolation (dots)', xlab='time or index')
points(x[,1]-mysum$resid)
grid()
dev.off()
bitmap(file='test1.png')
plot(mysum$resid, type='b', pch=19, main='Residuals', ylab='value of Residuals', xlab='time or index')
grid()
dev.off()
bitmap(file='test2.png')
hist(mysum$resid, main='Residual Histogram', xlab='values of Residuals')
grid()
dev.off()
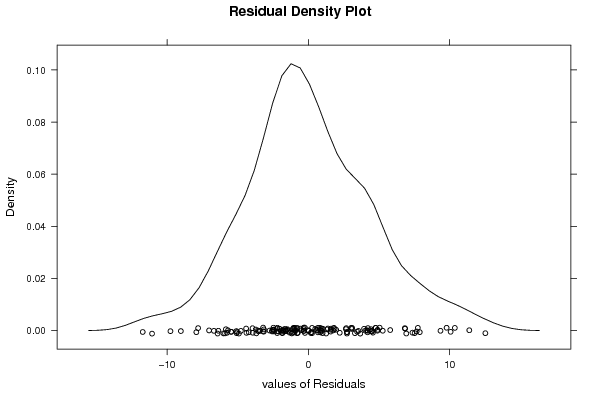
bitmap(file='test3.png')
densityplot(~mysum$resid,col='black',main='Residual Density Plot', xlab='values of Residuals')
dev.off()
bitmap(file='test4.png')
qqnorm(mysum$resid, main='Residual Normal Q-Q Plot')
qqline(mysum$resid)
grid()
dev.off()
(myerror <- as.ts(mysum$resid))
bitmap(file='test5.png')
dum <- cbind(lag(myerror,k=1),myerror)
dum
dum1 <- dum[2:length(myerror),]
dum1
z <- as.data.frame(dum1)
z
plot(z,main=paste('Residual Lag plot, lowess, and regression line'), ylab='values of Residuals', xlab='lagged values of Residuals')
lines(lowess(z))
abline(lm(z))
grid()
dev.off()
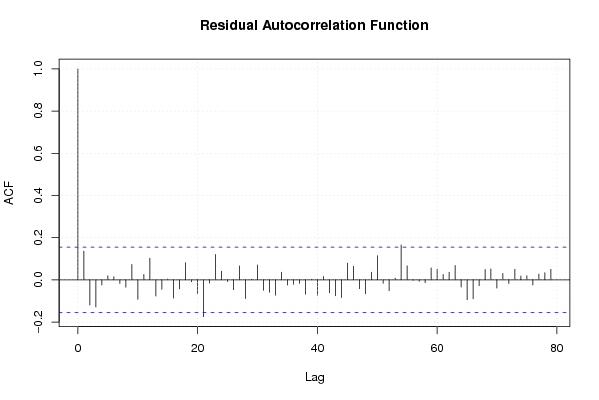
bitmap(file='test6.png')
acf(mysum$resid, lag.max=length(mysum$resid)/2, main='Residual Autocorrelation Function')
grid()
dev.off()
bitmap(file='test7.png')
pacf(mysum$resid, lag.max=length(mysum$resid)/2, main='Residual Partial Autocorrelation Function')
grid()
dev.off()
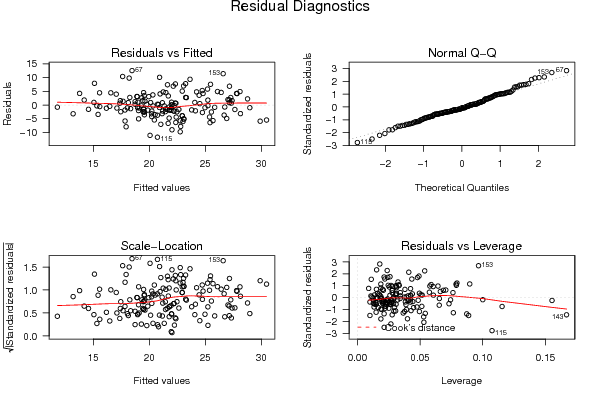
bitmap(file='test8.png')
opar <- par(mfrow = c(2,2), oma = c(0, 0, 1.1, 0))
plot(mylm, las = 1, sub='Residual Diagnostics')
par(opar)
dev.off()
if (n > n25) {
bitmap(file='test9.png')
plot(kp3:nmkm3,gqarr[,2], main='Goldfeld-Quandt test',ylab='2-sided p-value',xlab='breakpoint')
grid()
dev.off()
}
load(file='createtable')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a, 'Multiple Linear Regression - Estimated Regression Equation', 1, TRUE)
a<-table.row.end(a)
myeq <- colnames(x)[1]
myeq <- paste(myeq, '[t] = ', sep='')
for (i in 1:k){
if (mysum$coefficients[i,1] > 0) myeq <- paste(myeq, '+', '')
myeq <- paste(myeq, mysum$coefficients[i,1], sep=' ')
if (rownames(mysum$coefficients)[i] != '(Intercept)') {
myeq <- paste(myeq, rownames(mysum$coefficients)[i], sep='')
if (rownames(mysum$coefficients)[i] != 't') myeq <- paste(myeq, '[t]', sep='')
}
}
myeq <- paste(myeq, ' + e[t]')
a<-table.row.start(a)
a<-table.element(a, myeq)
a<-table.row.end(a)
a<-table.end(a)
table.save(a,file='mytable1.tab')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,hyperlink('http://www.xycoon.com/ols1.htm','Multiple Linear Regression - Ordinary Least Squares',''), 6, TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'Variable',header=TRUE)
a<-table.element(a,'Parameter',header=TRUE)
a<-table.element(a,'S.D.',header=TRUE)
a<-table.element(a,'T-STAT<br />H0: parameter = 0',header=TRUE)
a<-table.element(a,'2-tail p-value',header=TRUE)
a<-table.element(a,'1-tail p-value',header=TRUE)
a<-table.row.end(a)
for (i in 1:k){
a<-table.row.start(a)
a<-table.element(a,rownames(mysum$coefficients)[i],header=TRUE)
a<-table.element(a,mysum$coefficients[i,1])
a<-table.element(a, round(mysum$coefficients[i,2],6))
a<-table.element(a, round(mysum$coefficients[i,3],4))
a<-table.element(a, round(mysum$coefficients[i,4],6))
a<-table.element(a, round(mysum$coefficients[i,4]/2,6))
a<-table.row.end(a)
}
a<-table.end(a)
table.save(a,file='mytable2.tab')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a, 'Multiple Linear Regression - Regression Statistics', 2, TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'Multiple R',1,TRUE)
a<-table.element(a, sqrt(mysum$r.squared))
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'R-squared',1,TRUE)
a<-table.element(a, mysum$r.squared)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'Adjusted R-squared',1,TRUE)
a<-table.element(a, mysum$adj.r.squared)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'F-TEST (value)',1,TRUE)
a<-table.element(a, mysum$fstatistic[1])
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'F-TEST (DF numerator)',1,TRUE)
a<-table.element(a, mysum$fstatistic[2])
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'F-TEST (DF denominator)',1,TRUE)
a<-table.element(a, mysum$fstatistic[3])
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'p-value',1,TRUE)
a<-table.element(a, 1-pf(mysum$fstatistic[1],mysum$fstatistic[2],mysum$fstatistic[3]))
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'Multiple Linear Regression - Residual Statistics', 2, TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'Residual Standard Deviation',1,TRUE)
a<-table.element(a, mysum$sigma)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'Sum Squared Residuals',1,TRUE)
a<-table.element(a, sum(myerror*myerror))
a<-table.row.end(a)
a<-table.end(a)
table.save(a,file='mytable3.tab')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a, 'Multiple Linear Regression - Actuals, Interpolation, and Residuals', 4, TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'Time or Index', 1, TRUE)
a<-table.element(a, 'Actuals', 1, TRUE)
a<-table.element(a, 'Interpolation<br />Forecast', 1, TRUE)
a<-table.element(a, 'Residuals<br />Prediction Error', 1, TRUE)
a<-table.row.end(a)
for (i in 1:n) {
a<-table.row.start(a)
a<-table.element(a,i, 1, TRUE)
a<-table.element(a,x[i])
a<-table.element(a,x[i]-mysum$resid[i])
a<-table.element(a,mysum$resid[i])
a<-table.row.end(a)
}
a<-table.end(a)
table.save(a,file='mytable4.tab')
if (n > n25) {
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'Goldfeld-Quandt test for Heteroskedasticity',4,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'p-values',header=TRUE)
a<-table.element(a,'Alternative Hypothesis',3,header=TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'breakpoint index',header=TRUE)
a<-table.element(a,'greater',header=TRUE)
a<-table.element(a,'2-sided',header=TRUE)
a<-table.element(a,'less',header=TRUE)
a<-table.row.end(a)
for (mypoint in kp3:nmkm3) {
a<-table.row.start(a)
a<-table.element(a,mypoint,header=TRUE)
a<-table.element(a,gqarr[mypoint-kp3+1,1])
a<-table.element(a,gqarr[mypoint-kp3+1,2])
a<-table.element(a,gqarr[mypoint-kp3+1,3])
a<-table.row.end(a)
}
a<-table.end(a)
table.save(a,file='mytable5.tab')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'Meta Analysis of Goldfeld-Quandt test for Heteroskedasticity',4,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'Description',header=TRUE)
a<-table.element(a,'# significant tests',header=TRUE)
a<-table.element(a,'% significant tests',header=TRUE)
a<-table.element(a,'OK/NOK',header=TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'1% type I error level',header=TRUE)
a<-table.element(a,numsignificant1)
a<-table.element(a,numsignificant1/numgqtests)
if (numsignificant1/numgqtests < 0.01) dum <- 'OK' else dum <- 'NOK'
a<-table.element(a,dum)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'5% type I error level',header=TRUE)
a<-table.element(a,numsignificant5)
a<-table.element(a,numsignificant5/numgqtests)
if (numsignificant5/numgqtests < 0.05) dum <- 'OK' else dum <- 'NOK'
a<-table.element(a,dum)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'10% type I error level',header=TRUE)
a<-table.element(a,numsignificant10)
a<-table.element(a,numsignificant10/numgqtests)
if (numsignificant10/numgqtests < 0.1) dum <- 'OK' else dum <- 'NOK'
a<-table.element(a,dum)
a<-table.row.end(a)
a<-table.end(a)
table.save(a,file='mytable6.tab')
}
| | |
Copyright

This work is licensed under a
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License.
Software written by Ed van Stee & Patrick Wessa
Disclaimer
Information provided on this web site is provided
"AS IS" without warranty of any kind, either express or implied,
including, without limitation, warranties of merchantability, fitness
for a particular purpose, and noninfringement. We use reasonable
efforts to include accurate and timely information and periodically
update the information, and software without notice. However, we make
no warranties or representations as to the accuracy or
completeness of such information (or software), and we assume no
liability or responsibility for errors or omissions in the content of
this web site, or any software bugs in online applications. Your use of
this web site is AT YOUR OWN RISK. Under no circumstances and under no
legal theory shall we be liable to you or any other person
for any direct, indirect, special, incidental, exemplary, or
consequential damages arising from your access to, or use of, this web
site.
Privacy Policy
We may request personal information to be submitted to our servers in order to be able to:
- personalize online software applications according to your needs
- enforce strict security rules with respect to the data that you upload (e.g. statistical data)
- manage user sessions of online applications
- alert you about important changes or upgrades in resources or applications
We NEVER allow other companies to directly offer registered users
information about their products and services. Banner references and
hyperlinks of third parties NEVER contain any personal data of the
visitor.
We do NOT sell, nor transmit by any means, personal information, nor statistical data series uploaded by you to third parties.
We carefully protect your data from loss, misuse, alteration,
and destruction. However, at any time, and under any circumstance you
are solely responsible for managing your passwords, and keeping them
secret.
We store a unique ANONYMOUS USER ID in the form of a small
'Cookie' on your computer. This allows us to track your progress when
using this website which is necessary to create state-dependent
features. The cookie is used for NO OTHER PURPOSE. At any time you may
opt to disallow cookies from this website - this will not affect other
features of this website.
We examine cookies that are used by third-parties (banner and
online ads) very closely: abuse from third-parties automatically
results in termination of the advertising contract without refund. We
have very good reason to believe that the cookies that are produced by
third parties (banner ads) do NOT cause any privacy or security risk.
FreeStatistics.org is safe. There is no need to download any
software to use the applications and services contained in this
website. Hence, your system's security is not compromised by their use,
and your personal data - other than data you submit in the account
application form, and the user-agent information that is transmitted by
your browser - is never transmitted to our servers.
As a general rule, we do not log on-line behavior of
individuals (other than normal logging of webserver 'hits'). However,
in cases of abuse, hacking, unauthorized access, Denial of Service
attacks, illegal copying, hotlinking, non-compliance with international
webstandards (such as robots.txt), or any other harmful behavior, our
system engineers are empowered to log, track, identify, publish, and
ban misbehaving individuals - even if this leads to ban entire blocks
of IP addresses, or disclosing user's identity.
FreeStatistics.org is powered by
|










