• QR Code (size=2)
• QR Code (size=3)
• QR Code (size=4)
• QR Code (size=5)
• QR Code (size=6)

92,3
95,5
92,5
89,6
84,3
76,3
80,7
96,3
81,0
82,9
90,3
74,8
70,1
86,7
86,4
89,9
88,1
78,8
81,1
85,4
82,6
80,3
81,2
68,0
67,4
91,3
94,9
82,8
88,6
73,1
76,7
93,2
84,9
83,8
93,5
91,9
69,6
87,0
90,2
82,7
91,4
74,6
76,1
87,1
78,4
81,3
99,3
71,0
73,2
95,6
84,0
90,8
93,6
80,9
84,4
97,3
83,5
88,8
100,7
69,4
74,6
96,6
96,6
93,1
91,8
85,7
79,1
91,3
84,2
85,8
94,6
77,1
76,5

95,5
98,7
115,9
110,4
109,5
92,3
102,1
112,8
110,2
98,9
119,0
104,3
98,8
109,4
170,3
118,0
116,9
111,7
116,8
116,1
114,8
110,8
122,8
104,7
86,0
127,2
126,1
114,6
127,8
105,2
113,1
161,0
126,9
117,7
144,9
119,4
107,1
142,8
126,2
126,9
179,2
105,3
114,8
125,4
113,2
134,4
150,0
100,9
101,8
137,7
138,7
135,4
153,8
119,5
123,3
166,4
137,5
142,2
167,0
112,3
120,6
154,9
153,4
156,2
175,8
131,7
130,1
161,1
128,2
140,3
174,9
111,8
136,6

79,3
117,2
116,9
120,8
96,1
100,8
105,3
116,1
112,8
114,5
117,2
77,1
80,1
120,3
133,4
109,4
93,2
91,2
99,2
108,2
101,5
106,9
104,4
77,9
60,0
99,5
95,0
105,6
102,5
93,3
97,3
127,0
111,7
96,4
133,0
72,2
95,8
124,1
127,6
110,7
104,6
112,7
115,3
139,4
119,0
97,4
154,0
81,5
88,8
127,7
105,1
114,9
106,4
104,5
121,6
141,4
99,0
126,7
134,1
81,3
88,6
132,7
132,9
134,4
103,7
119,7
115,0
132,9
108,5
113,9
142,0
97,7
92,2

x <- array(x,dim=c(length(x),1))
colnames(x) <- par5
y <- array(y,dim=c(length(y),1))
colnames(y) <- par6
z <- array(z,dim=c(length(z),1))
colnames(z) <- par7
d <- data.frame(cbind(z,y,x))
colnames(d) <- list(par7,par6,par5)
par1 <- as.numeric(par1)
par2 <- as.numeric(par2)
if (par1>500) par1 <- 500
if (par2>500) par2 <- 500
if (par1<10) par1 <- 10
if (par2<10) par2 <- 10
library(GenKern)
library(lattice)
panel.hist <- function(x, ...)
{
usr <- par('usr'); on.exit(par(usr))
par(usr = c(usr[1:2], 0, 1.5) )
h <- hist(x, plot = FALSE)
breaks <- h$breaks; nB <- length(breaks)
y <- h$counts; y <- y/max(y)
rect(breaks[-nB], 0, breaks[-1], y, col='black', ...)
}
bitmap(file='cloud1.png')
cloud(z~x*y, screen = list(x=-45, y=45, z=35),xlab=par5,ylab=par6,zlab=par7)
dev.off()
bitmap(file='cloud2.png')
cloud(z~x*y, screen = list(x=35, y=45, z=25),xlab=par5,ylab=par6,zlab=par7)
dev.off()
bitmap(file='cloud3.png')
cloud(z~x*y, screen = list(x=35, y=-25, z=90),xlab=par5,ylab=par6,zlab=par7)
dev.off()
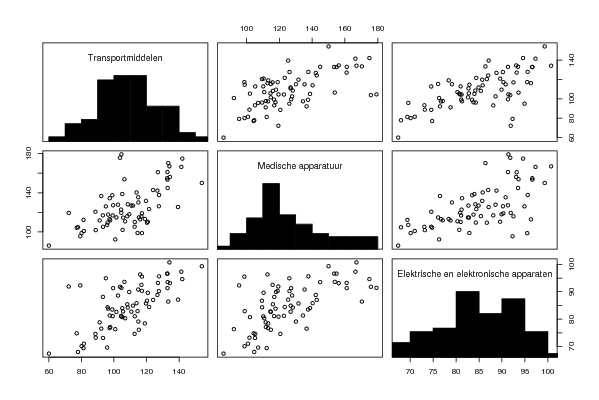
bitmap(file='pairs.png')
pairs(d,diag.panel=panel.hist)
dev.off()
x <- as.vector(x)
y <- as.vector(y)
z <- as.vector(z)
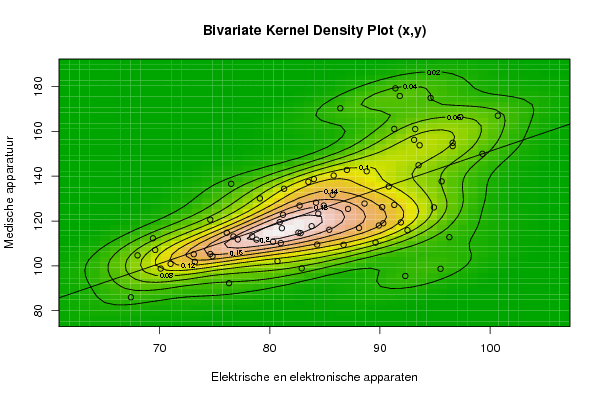
bitmap(file='bidensity1.png')
op <- KernSur(x,y, xgridsize=par1, ygridsize=par2, correlation=cor(x,y), xbandwidth=dpik(x), ybandwidth=dpik(y))
image(op$xords, op$yords, op$zden, col=terrain.colors(100), axes=TRUE,main='Bivariate Kernel Density Plot (x,y)',xlab=par5,ylab=par6)
if (par3=='Y') contour(op$xords, op$yords, op$zden, add=TRUE)
if (par4=='Y') points(x,y)
(r<-lm(y ~ x))
abline(r)
box()
dev.off()
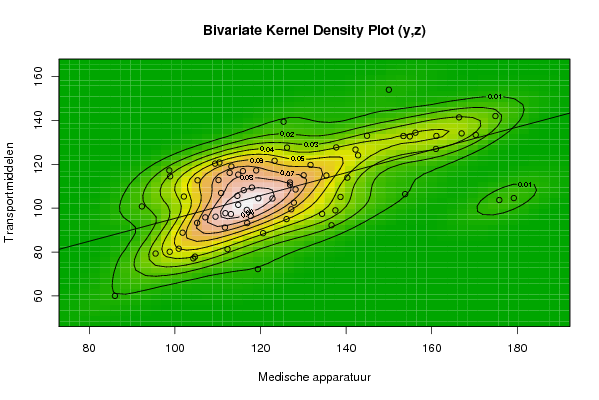
bitmap(file='bidensity2.png')
op <- KernSur(y,z, xgridsize=par1, ygridsize=par2, correlation=cor(y,z), xbandwidth=dpik(y), ybandwidth=dpik(z))
op
image(op$xords, op$yords, op$zden, col=terrain.colors(100), axes=TRUE,main='Bivariate Kernel Density Plot (y,z)',xlab=par6,ylab=par7)
if (par3=='Y') contour(op$xords, op$yords, op$zden, add=TRUE)
if (par4=='Y') points(y,z)
(r<-lm(z ~ y))
abline(r)
box()
dev.off()
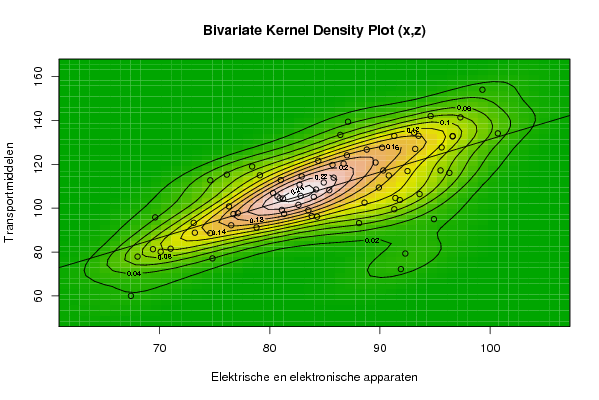
bitmap(file='bidensity3.png')
op <- KernSur(x,z, xgridsize=par1, ygridsize=par2, correlation=cor(x,z), xbandwidth=dpik(x), ybandwidth=dpik(z))
op
image(op$xords, op$yords, op$zden, col=terrain.colors(100), axes=TRUE,main='Bivariate Kernel Density Plot (x,z)',xlab=par5,ylab=par7)
if (par3=='Y') contour(op$xords, op$yords, op$zden, add=TRUE)
if (par4=='Y') points(x,z)
(r<-lm(z ~ x))
abline(r)
box()
dev.off()