• QR Code (size=2)
• QR Code (size=3)
• QR Code (size=4)
• QR Code (size=5)
• QR Code (size=6)

25
25
19
18
18
22
29
26
25
23
23
23
24
30
19
24
32
30
29
17
25
26
26
25
23
21
19
35
19
20
21
21
24
23
19
17
24
15
25
27
29
27
18
25
22
26
23
16
27
25
14
19
20
16
18
22
21
22
22
32
23
31
18
23
26
24
19
14
20
22
24
25
21
28
24
20
21
23
13
24
21
21
17
14
29
25
16
25
25
21
23
22
19
24
26
25
20
22
14
20
32
21
22
28
25
17
21
23
27
22
19
20
17
24
21
21
23
24
19
22
26
17
17
19
15
17
27
19
21
25
19
22
18
20
15
20
29
19
29
24
23
22
23
22
29
26
26
21
18
10

14
18
11
12
16
18
14
14
15
15
17
19
10
18
14
14
17
14
16
18
14
12
17
9
16
14
11
16
13
17
15
14
16
9
15
17
13
15
16
16
12
12
11
15
17
13
16
14
11
12
12
15
16
15
12
12
8
13
11
14
15
10
11
12
15
15
14
16
15
15
13
17
13
15
13
15
16
15
16
15
14
15
7
17
13
15
14
13
16
12
14
17
15
17
12
16
11
15
9
16
10
10
15
11
13
14
18
16
14
14
14
14
12
14
15
15
15
13
17
17
19
15
13
9
15
15
16
11
14
11
15
13
15
16
14
15
16
16
11
13
16
12
9
13
13
14
19
13
12
13

par1 <- as.numeric(par1)
library(lattice)
z <- as.data.frame(cbind(x,y))
m <- lm(y~x)
summary(m)
bitmap(file='test1.png')
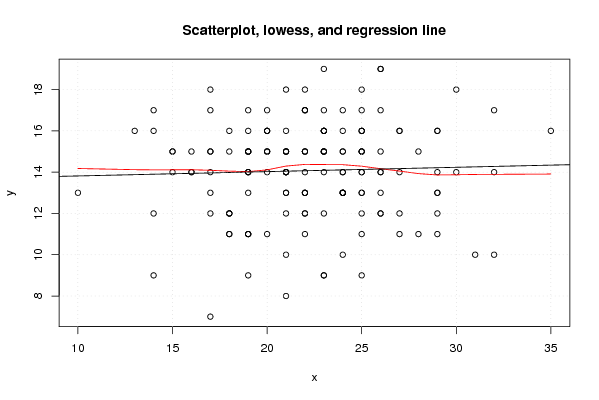
plot(z,main='Scatterplot, lowess, and regression line')
lines(lowess(z),col='red')
abline(m)
grid()
dev.off()
bitmap(file='test2.png')
m2 <- lm(m$fitted.values ~ x)
summary(m2)
z2 <- as.data.frame(cbind(x,m$fitted.values))
names(z2) <- list('x','Fitted')
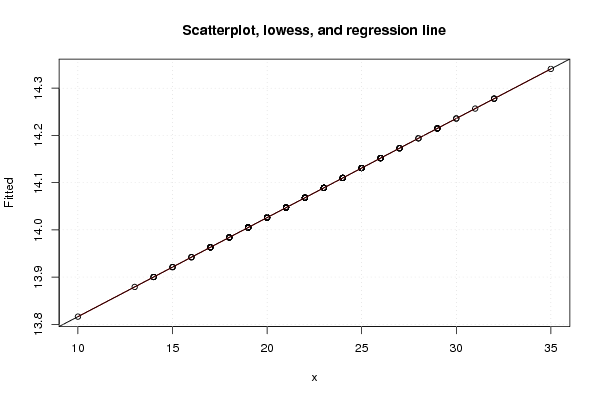
plot(z2,main='Scatterplot, lowess, and regression line')
lines(lowess(z2),col='red')
abline(m2)
grid()
dev.off()
bitmap(file='test3.png')
m3 <- lm(m$residuals ~ x)
summary(m3)
z3 <- as.data.frame(cbind(x,m$residuals))
names(z3) <- list('x','Residuals')
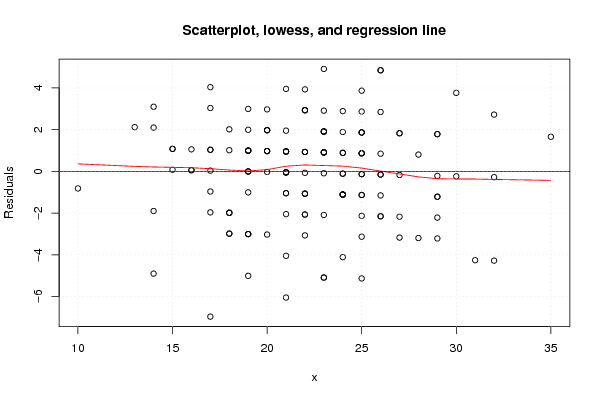
plot(z3,main='Scatterplot, lowess, and regression line')
lines(lowess(z3),col='red')
abline(m3)
grid()
dev.off()
bitmap(file='test4.png')
m4 <- lm(m$fitted.values ~ m$residuals)
summary(m4)
z4 <- as.data.frame(cbind(m$residuals,m$fitted.values))
names(z4) <- list('Residuals','Fitted')
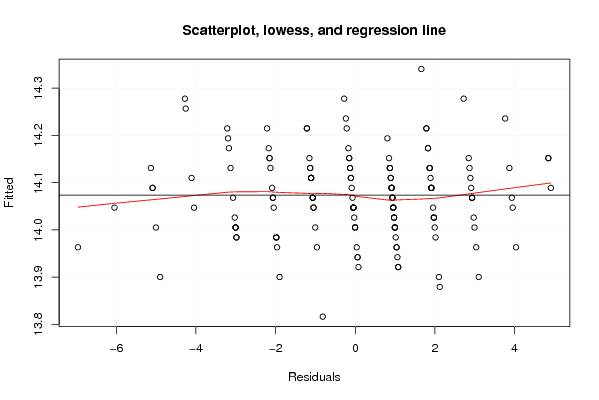
plot(z4,main='Scatterplot, lowess, and regression line')
lines(lowess(z4),col='red')
abline(m4)
grid()
dev.off()
bitmap(file='test5.png')
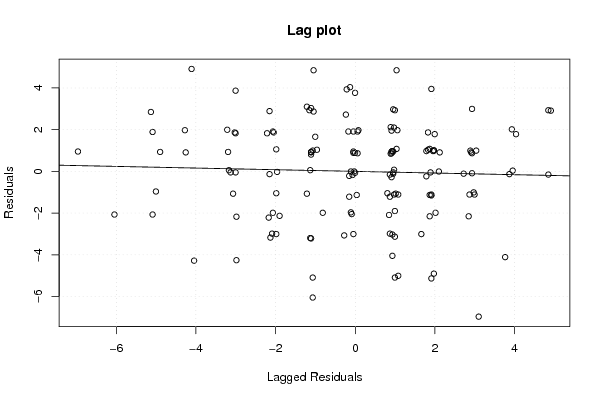
myr <- as.ts(m$residuals)
z5 <- as.data.frame(cbind(lag(myr,1),myr))
names(z5) <- list('Lagged Residuals','Residuals')
plot(z5,main='Lag plot')
m5 <- lm(z5)
summary(m5)
abline(m5)
grid()
dev.off()
bitmap(file='test6.png')
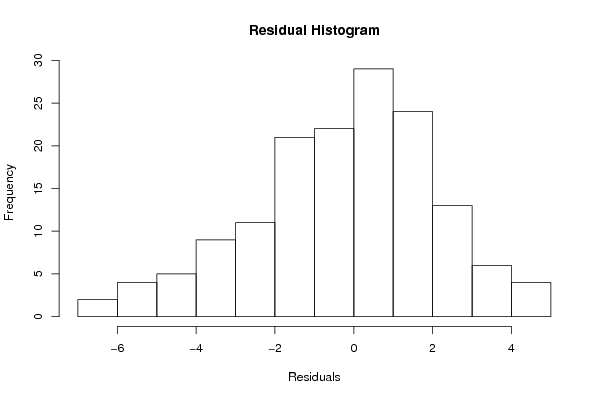
hist(m$residuals,main='Residual Histogram',xlab='Residuals')
dev.off()
bitmap(file='test7.png')
if (par1 > 0)
{
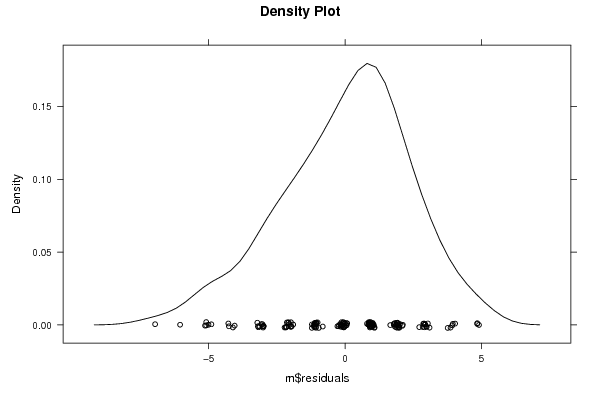
densityplot(~m$residuals,col='black',main=paste('Density Plot   bw = ',par1),bw=par1)
} else {
densityplot(~m$residuals,col='black',main='Density Plot')
}
dev.off()
bitmap(file='test8.png')
acf(m$residuals,main='Residual Autocorrelation Function')
dev.off()
bitmap(file='test9.png')
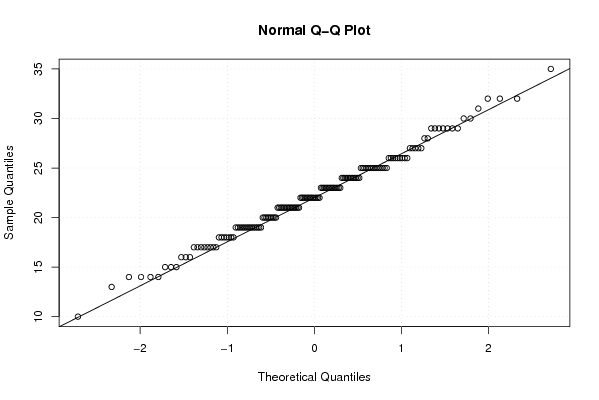
qqnorm(x)
qqline(x)
grid()
dev.off()
load(file='createtable')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'Simple Linear Regression',5,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'Statistics',1,TRUE)
a<-table.element(a,'Estimate',1,TRUE)
a<-table.element(a,'S.D.',1,TRUE)
a<-table.element(a,'T-STAT (H0: coeff=0)',1,TRUE)
a<-table.element(a,'P-value (two-sided)',1,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'constant term',header=TRUE)
a<-table.element(a,m$coefficients[[1]])
sd <- sqrt(vcov(m)[1,1])
a<-table.element(a,sd)
tstat <- m$coefficients[[1]]/sd
a<-table.element(a,tstat)
pval <- 2*(1-pt(abs(tstat),length(x)-2))
a<-table.element(a,pval)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'slope',header=TRUE)
a<-table.element(a,m$coefficients[[2]])
sd <- sqrt(vcov(m)[2,2])
a<-table.element(a,sd)
tstat <- m$coefficients[[2]]/sd
a<-table.element(a,tstat)
pval <- 2*(1-pt(abs(tstat),length(x)-2))
a<-table.element(a,pval)
a<-table.row.end(a)
a<-table.end(a)
table.save(a,file='mytable.tab')