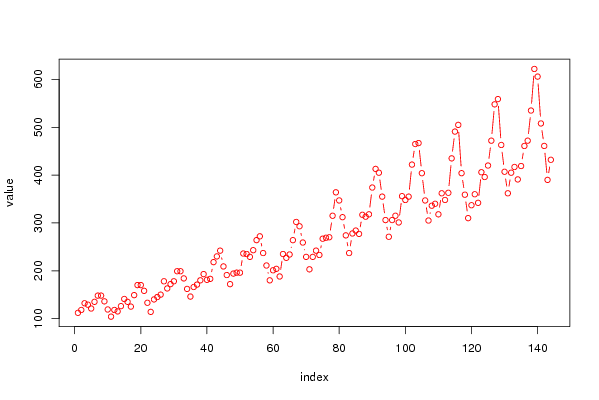
| 2008-12-07 12:51:22 [Jolien Van Landeghem] | [reply] | De waarden vind je via de variance reduction matrix. Vervolgens vul je deze waarden in. Je onderzoekt vervolgens 3 dingen : de autocorrelatie, de variance reduction matrix en de spectraal analyse. Je zou moeten vaststellen dat bij elke methode je op d=1 en D= 1 komt. antw :Hier gaan we proberen de tijdreeks stationair te maken. Je bekomt hier de correlatie tussen de tijdreeks en de tijdreeks in een vorige periode of een toekomstige periode. Zo is 0.94 de correlatie tussen yt en y(t-1). Op de autocorrelation function zie je een dalend verloop in de tijdreeks. Je stelt hier duidelijk de seizoenaliteit vast (er is sprake van een hangmatpatroon). Om de 12 maanden krijk je een opwaartse sprong.
Als we de tijdreeks gaan proberen stationair te maken, door te differentiëren met d=1 zie je duidelijk dat de dalende trend zo goed als weg is. Seizoenaliteit is er echter nog steeds en je kan ook vaststellen dat er een dalend patroon zit in de seizoenale autocorrelatie (door bijvoorbeeld 60 perioden te kiezen).
Als we d=1 en D=1 instellen krijgen we wel een stationaire tijdreeks
Specraal analyse : we gaan hier de tijdreeks ontbinden in golfbewegingen. We stellen hier duidelijk seizoenaliteit vast, op tijdstip 12 of 6 of 24 stel je een hogere intensiteit vast. Je stelt ook vast dat de kortere perioden minder belangrijk zijn dn de eerste periode van 144 maanden, want dit kent een hoge intensiteit. Ook stellen we hier een trend vast de meest dominante heeft de langste periode. Bij de variance reduction matrix bekom je dezelfde conclusie. | |
| 2008-12-08 18:54:30 [Nathalie Daneels] | [reply] | Evaluatie Q5 en Q6.
Ik ga hier beide vragen evalueren wnt telkens ik de link van Q5 aanklik, krijg ik de melding dat deze link foutief is.
Evaluatie Q5:
De student vermeldde hier dat hij/zij de differentiatie niet kon, maar er moet hier helemaal geen differentiatie gedaan worden. De grafiek van de Standard Deviation-Mean Plot is correct, maar de tabellen zouden ook moeten worden opgenomen bij deze vraag. De eerste tabel is de tabel met als titel 'Standard Deviation mean plot' en de tweede tabel, is de tabel met de titel 'Regression: S.E.(k) = alpha + beta * Mean(k)'. De derde tabel heeft als titel 'Regression: ln S.E.(k) = alpha + beta * ln Mean(k)'.
Dit zou de conclusie kunnen zijn:
Definitie van Standard Deviation-Mean Plot: is de scatterplot van de standaarddeviatie versus het gemiddelde van sequentiële delen/periodes/secties van de tijdreeks. Elk deel/periode/sectie bevat hetzelfde nummer van observaties, waarbij de voorkeur wordt gegeven aan s periodes (s = 12 voor maandelijkse tijdreeksen). De regressielijn van de SMP toont aan hoe de standaarddeviatie gerelateerd is aan het niveau (het gemiddelde) van de tijdreeks.
De lambda-transformatie van een tijdreeks: dit is een mathematische functie die, als ze behoorlijk wordt gebruikt, de stabiliteit van de standaarddeviatie kan veroorzaken (de tweede voorwaarde van stationariteit tegemoet komen/bevredigen).
Als we naar de eerste grafiek kijken, kunnen we vaststellen dat er duidelijke schommelingen zijn op korte termijn. Dit wijst op seizoenaliteit. Daarenboven heb ik het vermoeden dat er ook een lange termijn trend aanwezig is in de grafiek (Een stijgende lange termijn trend).
A.h.v. de Standard Deviation-Mean Plot kunnen de waarde vinden voor de parameter lamba. De waarde van deze lambda zorgt ervoor dat de variantie van de tijdreeks gestabiliseerd wordt. Deze methode gaat de tijdreeks, die we gaan bestuderen, onderverdelen in perioden (Hier: 12 maanden = seasonal period).
In de eerste tabel kunnen we zien dat er van elke maand het gemiddelde, de standaarddeviatie en de range wordt berekend.
We moeten ons de vraag stellen of er een verband bestaat tussen het niveau en de standaardfout? Is de spreiding afhankelijk van het niveau van de tijd?
Als we naar de laatste grafiek gaan kijken, kunnen we een besluit trekken of er al dan niet een verband bestaat tussen het niveau en de standaardfout. Uit de laatste grafiek kunnen we afleiden dat er een zeer duidelijk positief verband bestaat tussen het gemiddelde en de standaardfout. We kunnen hier zeer goed de regressierechte gebruiken om het verband te vinden/aan te tonen.
Uit de tweede tabel kunnen we afleiden dat alpha negatief is en bèta positief is. Als we bovendien naar de p-waarde kijken, kunnen we vaststellen dat er minder dan 1% kans is dat we ons vergissen bij het verwerpen van de Ho. We kunnen dus concluderen dat de helling van de grafiek niet aan het toeval te wijten is: Er is dus een verband tussen de standaardfout en het gemiddelde. A.h.v. deze tabel gaan we onderzoeken of er een verband bestaat tussen het gemiddelde en de standaardfout. Als dit zo is, dan mogen we de waarde van lambda gebruiken.
Als we naar de derde tabel gaan kijken, dan kunnen we merken dat de regressierechte opnieuw wordt berekend, maar dan in een getransformeerde/logaritmische vorm. Uit deze tabel kunnen we ook de waarde van lambda afleiden. Als lambda = 0, dan gaan we de transformatie ‘log’ nemen van de tijdreeks. Als lambda niet gelijk is aan 0, dan gaan we de tijdreeks tot de exponent lambda transformeren. Uit deze tabel kunnen we dus afleiden dat lambda afgerond ongeveer – 0,3 is.
Evaluatie bij Q6:
De student is er niet in geslaagd om deze vraag op te lossen. Ik zal hier de links opeenvolgend zetten die bij deze vraag horen. Opmerking: ik heb deze vraag stapsgewijs opgelost.
Dit zijn de links op volgorde:
* Eerst heb ik de ACF berekend:
- http://www.freestatistics.org/blog/index.php?v=date/2008/Dec/02/t1228252760g8nk67l7dc7clsu.htm
- http://www.freestatistics.org/blog/index.php?v=date/2008/Dec/02/t1228253074c1q4rnpc5j29dyi.htm
- http://www.freestatistics.org/blog/index.php?v=date/2008/Dec/02/t1228253248q7tehvpof4zxb1g.htm
- http://www.freestatistics.org/blog/index.php?v=date/2008/Dec/08/t1228762269gx0xpbwbk9nuthg.htm
* Berekening van de VRM:
- http://www.freestatistics.org/blog/index.php?v=date/2008/Dec/02/t1228253551gl3p0n653i2kzzo.htm
* Berekening van de spectraal analyse:
- http://www.freestatistics.org/blog/index.php?v=date/2008/Dec/02/t1228253952mgth450kbnsbm90.htm
- http://www.freestatistics.org/blog/index.php?v=date/2008/Dec/02/t122825415075r0ab6p8yxlovi.htm
- http://www.freestatistics.org/blog/index.php?v=date/2008/Dec/02/t12282544178nkre9epa3pmge5.htm
De conclusie hierbij is de volgende:
In de ‘time series analysis (new)’ vinden we alle modules die bruikbaar zijn om een tijdreeks te analyseren. We moeten bij deze vraag gebruik maken van 3 methodes/mogelijkheden: Autocorrelation function, Variance Reduction Matrix en Spectrum Analyse.
* De eerste methode (ACF): We gaan de tijdreeks stationair maken aan de hand van de autocorrelatiefunctie. Stationair maken houdt in dat we de lange termijn trend en/of de seizoenaliteit uit de tijdreeks gaan halen door een aantal keer te (seizoenaal) differentiëren en/of de tijdreeks te transformeren.
- We gaan eerst de tijdreeks bekijken, zonder daar een transformatie/differentiatie op te hebben toegepast (Lambda = 1, D = 0 en d = 0). In de tabel zien we in de tweede kolom ‘ACF(k)’ de 1e autocorrelatie (De autocorrelatie die overeenkomt met time lag 1): het verband tussen Yt en Yt-1, de 2e autocorrelatie (De autocorrelatie die overeenkomt met time lag 2): het verband tussen Yt en Yt-2,… Er wordt dus telkens het verband getoond tussen de waarden van de tijdreeks nu en de waarden van de tijdreeks in het verleden (Yt-1, Yt-2, waarbij Yt-1, de tijdreeks 1 periode wordt vertraagd, waarbij Yt-2, de tijdreeks 2 periodes wordt vertraagd,…).
Als we vervolgens naar de grafiek kijken, kunnen we vaststellen dat er een langzaam dalende functie is van allemaal positieve correlatiecoëfficiënten. Er is duidelijk zichtbaar dat een hangmattenpatroon zich voordoet. We merken dat de palen van deze hangmatten allemaal positieve en significante correlatiecoëfficiënten zijn en dat ze overeenkomen met de perioden 12,24,… (Telkens om het jaar) Dit wijst op seizoenaliteit. Dit hangmattenpatroon is (vaak) een typisch patroon voor een langzaam dalende ACF. Als we voornamelijk naar de linkse kant van de grafiek gaan kijken (Naar de eerste 4 à 5 coëfficiënten, waarbij de coëfficiënt die overeenkomt met lag 0 buiten beschouwing wordt gelaten), merken we een langzaam dalend patroon van positieve coëfficiënten die significant verschillend zijn van 0: Dit wijst erop dat er een lange termijn trend aanwezig is.
Om de tijdreeks stationair te maken, moeten we stapsgewijs te werk gaan.
- Om deze lange termijntrend weg te werken, moeten we de grafiek gaan differentiëren: We gaan d gelijk stellen aan 1 (Lambda blijft 1 en D = 0). We gaan merken dat de nieuwe grafiek er helemaal anders uit gaat zien. Waar we oorspronkelijk links een langzaam dalend patroon zagen, is dat er nu niet meer doordat we de tijdreeks hebben gedifferentieerd. Er is wel nog duidelijk seizoenaliteit aanwezig in de tijdreeks: De coëfficiënten die overeenkomen met de periodes 12, 24,… zijn positief en significant verschillend van 0.
- Als we dan vervolgens de ‘time lags’ wijzigen van 36 naar 60 dan kunnen we merken dat er opnieuw een langzaam dalend patroon is, maar dit enkel van de seizoenale correlatiecoëfficiënten (12,24,36,…). Door het aantal time lags te vergroten, gaan we de periodes (het aantal maanden/jaren) vergroten: Dit betekent dat we meer maanden/jaren in het verleden gaan kijken. Bij een tijdreeks waar seizoenaliteit aanwezig is, zoals in deze tijdreeks, betekent dit dat we 5 jaar (Time lags = 60 maanden = 5 jaar) van seizoenale autocorrelatie in het verleden kunnen opmerken/zien.
- Dit betekent dat we de tijdreeks bijkomend seizoenaal gaan moeten differentiëren: D = 1 (Lambda en d blijven 1) en als we de time lags behouden op 60, kunnen we merken op de nieuwe grafiek dat het langzaam dalend patroon van de seizoenale autocorrelatiecoëfficiënten volledig weg is. En de lange termijn trend was al in de 2e grafiek verdwenen. Dit betekent dat we erin geslaagd zijn om de tijdreeks stationair te maken (a.h.v. deze methode). Wat hebben we hieruit geleerd? Dat d = 1 en D = 1: Je moet de tijdreeks als volgt modelleren ‘N^d x N(12)^D x Yt = Et. Nu we weten wat D en d is kunnen we dit invullen in de formule: N x N(12) x Yt = Et. Als we dit vervolgens ingeven in de computer (die waardes van d en D en nadat we de waarde van lambda weten) dan krijgen we een differentievergelijking (N x N(12) x Yt = Et) waarmee we voorspellingen kunnen doen.
* De tweede mogelijkheid/methode is VRM (Variance Reduction Matrix): Dit is een zeer ruwe/eenvoudige manier om een analyse te maken. A.h.v. deze methode gaan we ook bepalen welke differentiatie nodig is om de tijdreeks stationair te maken. De eerste kolom van de tabel toont de soort van differentiatie/de combinatie van (al dan niet seizoenaal) differentiatie en in de tweede kolom vinden we de variantie van de tijdreeks, nadat deze gedifferentieerd is. In de tabel gaan we vervolgens kijken welke variantie het kleinste is: We kunnen uit de tabel afleiden dat we de kleinste variantie bekomen door Yt te differentiëren met d = 1 en D = 1. Dit hadden we ook gevonden met de autocorrelatiefunctie. Toch kan het soms zijn dat VRM en autocorrelatiefunctie niet overeen komen: Dan kunnen we best de autocorrelatiefunctie geloven omdat de VRM teveel beïnvloed kan worden door outliers. Nu als de tijdreeks veel outliers bevat (en die hebben een grote invloed op de variantie) dan kunnen we ook naar de laatste kolom in de tabel gaan kijken: Daar bevinden zich de getrimde varianties (de extreme outliers/ hoogste en laagste waarden zijn hierbij weggelaten, nadat de tijdreeks gedifferentieerd werd). Dus als je denkt dat uw tijdreeks outliers bevat, dan kunnen we best de laatste kolom bekijken.
* De derde methode/mogelijkheid is de Spectraal Analyse. Dit is een alternatieve methode van de ACF en VRM. M.b.v. deze methode gaan we dezelfde analyse maken: Hoeveel keer moeten we de tijdreeks (al dan niet seizoenaal) differentiëren om de dataset stationair te maken.
- Eerst gaan we geen transformatie doorvoeren op de tijdreeks. (Lambda = 1, D = 0 en d = 0). Bij deze methode wordt de tijdreeks ontbonden in regelmatige golfbewegingen/We gaan de regelmatige golfbewegingen uit de tijdreeks halen. De computer gaat de oorspronkelijke tijdreeks proberen te reconstrueren op basis van de golfbewegingen met verschillende frequenties (zie tabel). Die verschillende frequenties zeggen ons niet ; De periode daarentegen wel: Dit is dan ook de reden waarom de periode tussen haakjes erbij staat. Bijvoorbeeld: (144) = 144 maanden: Dit is de tijd die nodig is om 1 hele golf(beweging) te doen. De intensiteit van deze golfbewegingen wordt ook het spectrum genoemd: Dit geeft een indicatie van hoe sterk of minder sterk een golfbeweging is. We moeten hierbij opmerken dat als er een schommeling moest zijn rond deze golfbeweging: Dat deze schommeling niet sterk uitgesproken gaat zijn (die zal een kleinere amplitude hebben). Een golfbeweging met een lange periode wijst op een lange termijntrend. Als we uit de tabel/grafiek een cyclus kunnen opmerken van 12 maanden, dan wijst dit op seizoenaliteit. Uit de tabel kunnen we afleiden dat het overeenkomstig spectrum (van de golfbeweging met een periode van 12 maanden) = 68 000: Dit is een heel grote amplitude/sterk uitgesproken. We moeten in de tabel kijken wat er precies met kop en schouder bovenuit steekt: Welke spectrumwaarde voor de gegeven golfbeweging is het grootste? We kunnen uit de tabel afleiden dat dit is bij een periode van 12 maanden. Dit wordt ook bevestigd door de eerste grafiek: Ook daar wordt de hoogste waarde bereikt aan de linkse kant van de grafiek (Niet helemaal in het begin van de grafiek, maar toch redelijk in het begin).
Als we naar de tabel kijken, kunnen we opmerken dat er ook een groot spectrum is rond bijvoorbeeld 6 maanden. Als we uit de tabel kunnen afleiden dat er een regelmatige op- en neergaande fluctuatie is, die ongeveer op lange termijn aanwezig is (bv. Om de 6 maanden weer een piek in de waarde van het spectrum), dan wijst dit op een conjunctuurcyclus.
We kunnen eveneens uit de eerste grafiek afleiden dat er golfbewegingen met een zeer lange periode aanwezig zijn in de tijdreeks. Korte periodes komen overeen met hoge frequenties en lage frequenties (op de grafiek) komen overeen met lange termijnen/periodes: Deze lange periodes zijn belangrijk, de korte niet echt. Als er in de eerste grafiek positieve pieken zijn op regelmatige frequenties, dan wijzen die pieken op periodes met een hoog spectrum of m.a.w. op seizoenaliteit. Als er bijvoorbeeld bij 4 of 6 maanden ook een groot spectrum is, dan wijst dit op seizoenaliteit (want 6 maanden kunnen 2 keer in een jaar en 4 maanden kunnen 3 keer in een jaar).
Als we gaan kijken naar de cumulatieve periodogram: Een zeer stijle grafiek wijst op een lange termijn trend (verklaart 70% van de tijdreeks: Dat stukje rechte). Als er trappen in de grafiek aanwezig zijn, die wijzen op seizoenaliteit. In dit geval kunnen we dus concluderen dat er in de tijdreeks zowel seizoenaliteit als een lange termijn trend aanwezig is.
- We kunnen deze lange termijntrend wegwerken door te gaan differentiëren (d = 1). Als we dan opnieuw gaan kijken naar de periode van 144 maanden (in de tabel) dan kunnen we opmerken dat het spectrum kleiner is geworden (22,86). Op de eerste grafiek merken we dat er geen dalende of stijgende lijn meer is, maar een plus/minus horizontale lijn. Dit betekent dat de lange termijn trend ‘verwijderd’ is. We moeten wel opmerken dat er nog steeds positieve pieken aanwezig zijn in de grafiek en die wijzen dus op seizoenaliteit. Bij de grafiek ‘Cumulative periodogram’ kunnen we zien dat de stijlheid van de grafiek verdwenen is, maar het trappenpatroon is nog steeds heel duidelijk aanwezig. Dit betekent dat er nog steeds seizoenaliteit aanwezig is in de tijdreeks.
- Om de seizoenaliteit vervolgens weg te werken gaan we seizoenaal differentiëren (D = 1): Hierdoor gaan ook de pieken in de eerste grafiek plus/minus wegvallen. Als we dan ten slotte opnieuw gaan kijken naar de Cumulatieve periodogram dan merken we dat de grafiek niet helemaal binnen het betrouwbaarheidsinterval ligt: Dit wijst erop dat het niet aan het toeval kan worden toegeschreven. Het kan enkel aan het toeval worden toegeschreven als de grafiek helemaal binnen het betrouwbaarheidsinterval zou liggen (Dan zou het een rechte lijn (random)/diagonaal zijn tussen het interval). Het betrouwbaarheidsinterval is een indicatie van toeval. Het feit dat de grafiek nog steeds een beetje buiten het betrouwbaarheidsinterval van 95% ligt, wijst erop dat er nog golfbewegingen zijn in de tijdreeks, die verklaarbaar zijn/ dat er nog patronen aanwezig zijn in de tijdreeks, die voorspelbaar zijn. We kunnen dus concluderen dat het model nog voor verbetering vatbaar is: Het restdeel is nog niet aan het toeval geheel te wijzen.
| |
Post a new message |