| 2008-12-06 14:25:41 [Nicolaj Wuyts] | [reply] | | Uit de raw periodogram kunnen we afleiden dat er sprake is van een langetermijn trend. Dit kunnen we herkennen doordat er dalend trend is op lange termijn. In de cumulative periodogram kunnen we deze trend zien terugkomen. In het begin van periodogram zien we een stijle lijn lopen. Deze verklaard de lanetermijn trend. We zien ook dat 80% van de datareeks kan verklaard worden door deze trend. We kunnen echter ook nog een seizoenale trend ontdekken. Vanaf 0,8 zien we een getrapt verloop in het cumulatieve periodogram. Deze verklaart de trend. | |
| 2008-12-07 12:37:15 [Jolien Van Landeghem] | [reply] | | Op het periodogram zien we inderdaad dat er een trend is waarbij er geen stationariteit in het gemiddelde is ( in het begin stijl naar boven) end at er geen sprake is van seizoenaliteit (want er zijn geen trapjes) we gaan dit stationair maken door gebruik te maken van differentiatie met d=1 en D=0. Je kan ook vaststellen op het periodogram dat 80% verklaard kan worden adhv de trend. | |
| 2008-12-08 13:09:40 [Hundra Smet] | [reply] | de student gaf een zeer korte beschrijving (dat het ging om een LT verloop) bij de grafiek. dit kan uitgebreider:
Aan de hand van een spectraalanalyse gaan we de trend onderzoeken. Dit type van analyse wordt gebruikt om de sinus -en cosinusfuncties uit de tijdreeks te halen. Als er sprake is van een lange periode, is er sprake van een lage frequentie (want frequentie = 1/periode).
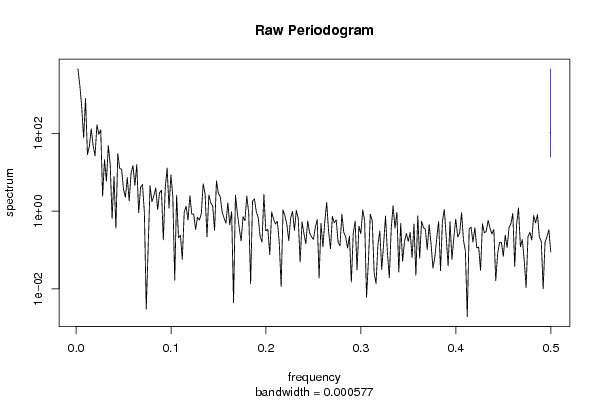
Kijken we naar het “Raw Periodogram” merken we duidelijk een langzaam dalende trend op.
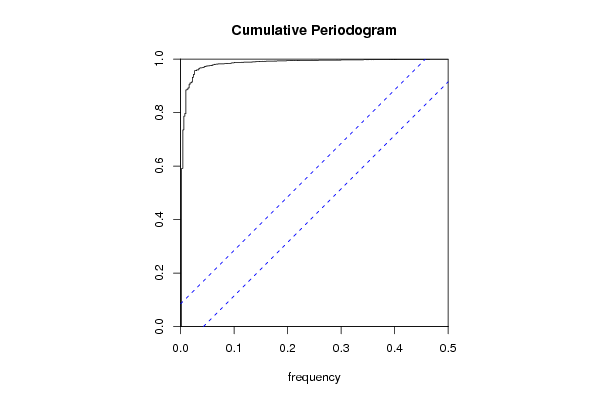
Vervolgens bestuderen we het cumulative periodogram. We kunnen duidelijk visueel waarnemen dat deze een zeer steil begin kent. Dit periodogram moet als volgt geïnterpreteerd worden: 80% van de datareeks kan verklaard worden door deze trend. Het is zo dat een steil stijgend cumulative periodogram wijst op aanwezigheid van een lange termijn trend.
We gaan dit stationair maken door gebruik te maken van differentiatie met d=1 en D=0. | |
| 2008-12-08 18:32:52 [Nathalie Daneels] | [reply] | Evaluatie opdracht 1 - Blok 17
Ik ga de evaluatie van Q1, Q2, Q3 en Q4 hierin zetten aangezien de student geen links had gezet bij de vragen Q1, Q2 en Q3.
Evaluatie Q1:
In de vraag staat dat er meerdere keren moet worden gereproduceerd. De student heeft dit hier maar 1 keer gedaan!
De conclusie die ik bij deze grafiek zou zetten is de volgende:
Als we het geheel intuïtief bekijken, kunnen we vaststellen dat er een schijnbaar trendmatig verloop, in dit geval een afwisselend stijgend, dalend en weer stijgend verloop (eerste grafiek van de twee), is dat voorspelbaar is. Maar de dalingen en stijgingen zijn puur aan het toeval te wijten. Bij deze technische analyse kunnen we ons afvragen of er patronen voorkomen in de tijdreeks. Wat het antwoord ook is (in dit geval ‘ja: stijging, daling, daarna weer een stijging), we mogen aan deze patronen geen betekenis hechten, want er zijn geen patronen in het verleden die het ons mogelijk maken om voorspellingen te doen. (Er is sprake van een patroon als er herhaling optreedt bv. Stijging, daling, stijging, daling,…). We moeten in het achterhoofd houden dat we met een simulatie bezig zijn. We kunnen dus vaststellen dat er geen seizoenaliteit en geen lange termijntrend is.
Algemene informatie die we bij deze vraag kunnen zetten:
De Random-Walk simulation heeft veel te maken met financiële markten. Veel economisten zeggen dat dit het model is voor de financiële markten: Het geeft de interpretatie van het mechanisme op de beurs (over de beurskoers).
We gaan bij deze workshop een simulatie-experiment doen met een muntstuk. Zoals iedereen weet heeft een muntstuk 2 zijden, namelijk kop en munt.
De eerste grafiek (van de 2 grafieken die per simulatie worden getoond) heeft als x-as het aantal keer dat er gegooid wordt met het muntstuk en als y-as hoe vaak de zijde kop meer wordt gegooid dan de zijde munt.
De tweede grafiek heeft als x-as eveneens het aantal keer dat er gegooid wordt met het muntstuk en als y-as de proportie van de zijde ‘kop’ van het muntstuk: We gaan hierbij relatief/proportioneel kijken: Op lange termijn gaat dit moeten convergeren naar 50%.
De modelvergelijking van dit fenomeen: Yt = Yt-1 + Et, waarbij (als we denken aan de toepassing op de financiële markten) Yt = beurkoers (de rode lijn in de eerste grafiek telkens), Yt-1 = de vorige beurskoers en Et = de toevalscomponent (1 of -1). Dit is het random walk model: Als dat model klopt en we willen een voorspelling maken van de beurskoers: Ft (= voorspelling): Yt – Et = Yt-1: We nemen de vorige voorspelling als voorspelling. Dit geeft als uitkomt een horizontale lijn. Dit gaan de beursanalisten niet toelaten: Zij gaan de beurskoers soms laten stijgen, als er in het verleden ergens ook al een stijgende trend is geweest. MAAR er is geen trend geweest, want dit was een simulatie: Hierbij is de trend onvoorspelbaar (Eigenlijk is ze wel voorspelbaar, maar dan is ze een horizontale lijn). Met een technische analyse kan je onmogelijk een stijgende of dalende lijn/trend voorspellen en evenmin seizoenaliteit.
Evaluatie bij Q2:
Even een kleine verbetering van interpretatie van de student: Als de correlatiecoëfficiënten bij de grafiek van de autocorrelatie buiten het betrouwbaarheidsinterval liggen, dan betekent dit dat ze significant verschillend zijn van nul en dus niet aan het toeval toe te schrijven zijn. En als er autocorrelatie optreedt, DAN betekent dit dat opeenvolgende waarden negatief of positief zijn. (Ze kunnen dus voorspeld worden op basis van het verleden).
De conclusie die ik bij deze grafieken zou zetten:
We gaan kijken of de autocorrelatiefunctie een bepaald patroon bevat. Hoe gaat die autocorrelatie functie eruit zien? We gaan een voorspelling proberen te maken: Is de beurskoers in een bepaalde periode relatief hoog/laag? Als je 2 opeenvolgende punten bekijkt in die periode: Zijn die dan allebei hoog/laag? Zo ja, dan kunnen we informatie halen uit het verleden: Als de vorige beurskoers zeer hoog is, dan is er een grote kans dat de volgende beurskoers ook zeer hoog gaat zijn. (Volgens onze voorspelling gaat de autocorrelatie functie vooral bestaan uit positieve autocorrelaties: Als de vorige waarde hoog is, dan gaat de volgende waarde ook hoog zijn.) Het voorgaande kan enkel gelden als Et (in de formule Yt = Yt-1 + Et) niet groot is of m.a.w. dat het niet aan het toeval kan worden toegeschreven of toch bijna niet. Als het niveau van de tijdreeks langzaam evolueert, dan krijgen we een positieve autocorrelatie. (<-> Als schommelingen zeer sterk zijn (jojo) en we dus een wispelturige grafiek gaan hebben, dan gaat de autocorrelatie negatief zijn.) Bij deze grafiek kunnen we opmerken dat er een langzaam dalend patroon is van de positieve autocorrelaties. Dit kunnen we concluderen door naar de eerste 4 à 5 correlatiecoëfficiënten te kijken (De correlatiecoëfficiënt op lag 0, moeten we buiten beschouwing laten). Als we deze eerste 5 coëfficiënten bekijken, kunnen we besluiten dat ze positief zijn en significant verschillend van 0. Dit kan niet toevallig zijn: Dat moet een fundamentele eigenschap hebben. Dat patroon is zeer typisch voor een stochastische trend op lange termijn (een niet lineaire/deterministische trend). Deze stochastische trend kan je modelleren/verwijderen door gebruik te maken van differentiatie.
Definitie van ACF: is de reeks van waarden die overeenkomen met de correlatie van de tijdreeks en zijn eigen verleden:
- De eerste waarde is de correlatie tussen Yt en Yt-1
- De tweede waarde is de correlatie tussen Yt en Yt-2
- …
Een operator wordt altijd toegepast op iets: Gaat de tijdreeks 1/s periode vertragen.
Bijvoorbeeld: Backshift-operator (Bs): Bs x Yt = Yt-s of B² x Yt = B x B x Yt = B x Yt-1 = Yt-2.
Bijvoorbeeld: Nabla-operator, Ns (Ik ga N nemen als teken voor Nabla, want ik vind de omgekeerde driehoek niet bij de symbolen), = (1 – Bs) of m.a.w. de Nabla-operator is per definitie gelijk aan (1 – Bs). Bijvoorbeeld: N x Yt = (1 – Bs) x Yt = Yt – Yt-1, waarbij N x Yt = differentiatie die we toepassen op de tijdreeks. Als we zien dat de autocorrelatiefunctie langzaam dalend is, dan: N x Yt = (1 – Bs) x Yt = Et
= Yt – Yt-1 = Et
= Yt = Yt-1 + Et. Dit is het Random – Walk model.
Hieruit kunnen we concluderen dat de Nabla – operator sterk gekoppeld is aan de definitie van het random walk model.
Evaluatie Q3:
De conclusie was niet juist bij de student.
Dit zou ik als conclusie zetten:
We gaan de gesimuleerde Random Walk tijdreeksen analyseren. Door gebruik te maken van de VRM gaan we nagaan welke differentiatie nodig is om de tijdreeks stationair te maken. Als we naar de tabel kijken, kunnen we opmerken dat er in de 1e kolom de (combinatie van) differentiatie staat/de soort van differentiatie. De tweede kolom bevat de varianties, nadat de tijdreeks (een aantal keer) gedifferentieerd hebben (op dit aantal keer differentiëren hebben d en D betrekking). Formule: N^d x Ns^D x Yt = Et met d = aantal keer dat we gewoon differentiëren/niet-seizoenaal differentiëren: Dit doen we om de lange termijn trend weg te werken, D heeft betrekking op seizoenaal differentiëren: We doen dit omdat er misschien seizoenaliteit is in de tijdreeks en die willen we weg en s duidt aan op 12 maanden in een jaar.
De variantiereductiematrix geeft de varianties van de tijdreeks, die telkens weer berekend wordt bij een nieuwe combinatie van D en d. Bijvoorbeeld: Yt (d=0, D=0): 54,8 (afgerond). Dit is de ruwe variantie: de variantie zonder dat de tijdreeks getransformeerd of (al dan niet seizoenaal) gedifferentieerd is. De variantie van Yt( d=1, D=0) is gelijk aan 1 (afgerond) en is de kleinste variantie. En zo kunnen we voor elke combinatie van d en D de (ruwe) variantie van Yt bepalen. Om te weten welke waarde van D en d we nodig hebben om de tijdreeks stationair te maken, moeten we gaan kijken waar de variantie het kleinst is: Bij d = 1 en D = 0, bij de tijdreeks 1 keer te differentiëren en niet seizoenaal te differentiëren.
Hier zit ook logica in: Als je de tijdreeks wilt verklaren, wil je ook zoveel mogelijk van de volatiliteit/risico verklaren: De variantie van de tijdreeks is de volatiliteit/risico dat in de tijdreeks zit. Dit willen we zo veel mogelijk verklaren: bijvoorbeeld we gaan de kleinste variantie uit de tijdreeks nemen (=1). Deze variantie komt overeen met een d van 1. Dit betekent dat we de tijdreeks 1 keer gaan differentiëren. Dus bij het bepalen welke waarde D en d moet hebben om de tijdreeks stationair te maken, gaan we kijken naar de kleinste variantie/het kleinste risico.
Bij een vermoeden dat er outliers aanwezig zijn in de tijdreeks, moeten we gaan kijken naar de getrimde variantie in de laatste kolom van de tabel. Dit is de variantie die berekend wordt, nadat de tijdreeks gedifferentieerd werd en de extreme (hoogste en laagste) waarden eruit werden gelaten.
Evaluatie Q4:
De conclusie bij de student is ruim onvoldoende.
Dit zou de conclusie kunnen zijn:
Spectral analysis is een methode om de trend van een tijdreeks te analyseren en is een alternatief van de ACF en VRM. A.h.v. deze methode, kunnen we dezelfde analyse maken over hoeveel keer de tijdreeks gedifferentieerd moet worden om de dataset stationair te maken. Spectrale analyse betekent dus dat we een tijdreeks hebben en dat we die gaan ontbinden. Dit gaan we dus toepassen op de Random Walk. We gaan dit voorspellen: Een lange termijn trend duidt op een lange periode en dus een kleine frequentie. We gaan dus golfbewegingen krijgen met een lage frequentie. Frequentie is het omgekeerde van de periode: Als de frequentie hoog is, dan gaat de periode laag zijn.
Grafiek ‘Raw periodogram’: Op de x-as staat de frequentie en op de y-as staat de intensiteit waarmee de golfbeweging voorkomt/het spectrum. We kunnen uit de grafiek afleiden dat het spectrum de hoogste waarden heeft in het begin/links van de grafiek (de hoogste y-waarden) of m.a.w. het spectrum domineert in het begin van de grafiek. We kunnen eveneens vaststellen dat de periode lang is (we merken een daling op van de grafiek), doordat er golfbewegingen met kleine frequenties aanwezig zijn in de grafiek/domineren.
In de grafiek zien we ook een aantal pieken: Als deze periodes, die overeenkomen met die pieken, gelijk zijn aan de jaartallen (12, 24,… maanden) of aan halfjaarlijkse periodes (6, 12, 18,… maanden) of aan kwartaalperiodes (4, 8, 12,… maanden), dan wijzen deze pieken op een vorm van seizoenaliateit. Of er al dan niet seizoenaliteit aanwezig is in de tijdreeks, kunnen we ook afleiden uit de cumulatieve periodogram.
De grafiek ‘Cumulative periodogram’ toont de optelling van alle intensiteiten (de cumulatieve intensiteit dus). We gaan dat schalen tussen 0 en 1 (op de y-as). Dit moeten we interpreteren zoals R-squared. Bijvoorbeeld 0,2 op de y-as betekent dat 20% van de tijdreeks kan worden verklaard. Bijvoorbeeld als we 80% van de tijdreeks willen verklaren, dan kunnen we op de grafiek zien dat dit overeenkomt met een frequentie van 0,03 (ongeveer). Dit wil dus zeggen dat de periode lang gaat zijn (want de frequentie is laag) of m.a.w. we hebben een lange termijn beweging nodig als we 80% van de tijdreeks willen verklaren. Een sterk stijgende grafiek wijst op een lange-termijn trend (Dat is daar een typisch kenmerk van): Een groot aantal van het percentage dat we willen verklaren, komt dan overeen met een lage frequentie, dus met een grote periode of een lange termijn trend. In dit geval is er niet echt sprake van seizoenaliteit in de grafiek: Er is seizoenaliteit als de grafiek trapjes vertoont, wat hier niet echt het geval is.
| |
Post a new message |